题目内容
【题目】在四边形ABCD中,已知AD//BC,∠ABC=90°.

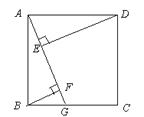
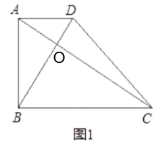
(1)若AC⊥BD,且AC=5,BD=3(如图1),求四边形ABCD的面积;
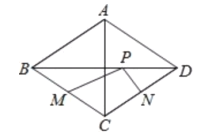
(2)若DE⊥BC于E,F是CD的中点,BD=BC,(如图2),求证:∠BAF=∠BCD.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)利用S四边形ABCD=S△ABD+S△CBD计算,即可得出结论;
(2)先判断出△ADF≌△GCF,得出AF=FG,进而得出AF=BF=FG,最后利用互余即可得出结论;
解:(1)设AC,BD的交点为O,
∵AC⊥BD,BD=3,AC=5,
∴S四边形ABCD=S△ABD+S△CBD
=![]() BD×OA+
BD×OA+![]() BD×OC
BD×OC
=![]() BD(OA+OC)
BD(OA+OC)
=![]() BD×AC
BD×AC
=![]() ;
;
(2)如图2,延长AF,BC相交于G,连接BF,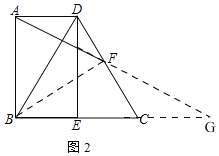
∵AD∥BC,∴∠DAF=∠CGF,
∵点F是CD的中点,
∴DF=CF,
在△ADF和△GCF中,
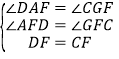
∴△ADF≌△GCF(AAS),
∴AF=GF,
∵∠ABC=90°,
∴∠G+∠BAF=90°,BF=AF=FG=![]() AG,
AG,
∴∠CBF=∠G,
∴∠CBF+∠BAF=90°,
∵BD=BC,CF=DF,
∴∠BFC=90°,
∴∠CBF+∠BCD=90°,
∴∠BAF=∠BCD;

练习册系列答案
相关题目