题目内容
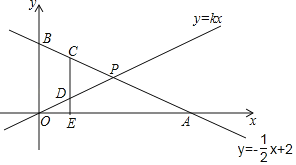
【题目】在平面直角坐标系xOy中,抛物线y=ax22a2x(a![]() 0)的对称轴与x轴交于点P.
0)的对称轴与x轴交于点P.
(1)求点P的坐标(用含a的代数式表示);
(2)记函数y=x+2(1![]() x
x![]() 2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
【答案】(1)(a,0);(2)a≤![]() 或a>0
或a>0
【解析】
(1)令y=0,求得抛物线与x轴的两个交点坐标,进而求得点P坐标;
(2)根据抛物线与图形M恰有一个公共点,结合图像可知当x=-1或当x=2时,这两个函数值的大小关系恰好相反,然后通过解不等式组即可求得a的取值范围.
解:(1)y=ax22a2x=ax(x2a)
令y=0,则x1=0,x2=2a,
∴对称轴为x=![]() ,
,
∴点P的坐标为(a,0)
(2)设y1=ax22a2x,y2=x+2(1![]() x
x![]() 2)
2)
∴当x=-1时,y1=a+2a2,y2=3,
当x=2时,y1=4a-4a2,y2=0,
∵抛物线与图形M恰有一个公共点,
∴抛物线与图形M如图所示:
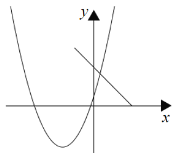


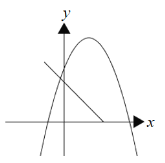
∴当a+2a2≥3时,4a-4a2≤0,
则2a2+a-3≥0,4a2-4a≥0,
∴(2a+3)(a-1)≥0①,4a(a-1)≥0②,
∴由①得,a≥1或a≤![]() ,
,
由②得,a≥1或a≤0,
∴a≥1或a≤![]() ,
,
当a+2a2≤3时,4a-4a2≥0,
则2a2+a-3≤0,4a2-4a≤0,
∴(2a+3)(a-1)≤0①,4a(a-1)≤0②,
∴由①得,![]() ≤a≤1,
≤a≤1,
由②得,0≤a≤1,
∴0≤a≤1,
∴a≤![]() 或a≥0,
或a≥0,
又∵a≠0,
∴a的取值范围是:a≤或a>0.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目