题目内容
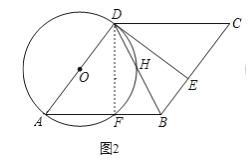
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
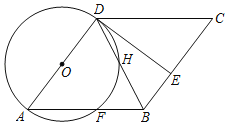
(1)求证:DE是⊙O的切线.
(2)若BF=2,BD=2![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)证明△DAF≌△DCE,可得∠DFA=∠DEC,证出∠ADE=∠DEC=90°,即OD⊥DE,DE是⊙O的切线.
(2)在Rt△ADF和Rt△BDF中,可得AD2-(AD-BF)2=DB2-BF2,解方程可求出AD的长即可.
(1)证明:如图1,连接DF,

∵四边形ABCD为菱形,
∴AB=BC=CD=DA,AD∥BC,∠DAB=∠C,
∵BF=BE,
∴AB﹣BF=BC﹣BE,
即AF=CE,
∴△DAF≌△DCE(SAS),
∴∠DFA=∠DEC,
∵AD是⊙O的直径,
∴∠DFA=90°,
∴∠DEC=90°
∵AD∥BC,
∴∠ADE=∠DEC=90°,
∴OD⊥DE,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)解:如图2,
∵AD是⊙O的直径,
∴∠DFA=90°,
∴∠DFB=90°,
在Rt△ADF和Rt△BDF中,
∵DF2=AD2﹣AF2,DF2=BD2﹣BF2,
∴AD2﹣AF2=DB2﹣BF2,
∴AD2﹣(AD﹣BF)2=DB2﹣BF2,
∴![]()
∴AD=5.
∴⊙O的半径为![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】某超市用3400元购进A、B两种文具盒共120个,这两种文具盒的进价、标价如下表:
价格/类型 | A型 | B型 |
进价(元/只) | 15 | 35 |
标价(元/只) | 25 | 50 |
(1)这两种文具盒各购进多少只?
(2)若A型文具盒按标价的9折出售,B型文具盒按标价的8折出售,那么这批文具盒全部售出后,超市共获利多少元?