Question

1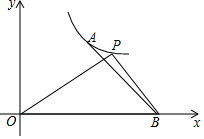．如图，已知反比例函数y=$\frac{k}{x}$（k≠0）图象经过点A（3，4），点B（6，0）在x轴正半轴上．
（1）求反比例函数解析式；
（2）点P（x，y）在反比例函数y=$\frac{k}{x}$图象上，当S_△POB=2S_△AOB时，求点P的坐标；
（3）点C在x轴上，当△ACB是等腰三角形时，求点C的坐标．

Answer 1

分析 （1）利用待定系数法求出反比例函数解析式；
（2）设点P的坐标为（x，$\frac{12}{x}$），根据三角形的面积公式列出方程，解方程即可；
（3）分AC=AB、CA=CB、BA=BC三种情况，根据等腰三角形的性质计算即可．

解答 解：（1）∵反比例函数y=$\frac{k}{x}$图象经过点A（3，4），
∴4=$\frac{k}{3}$，
解得，k=12，
则反比例函数解析式为y=$\frac{12}{x}$；
（2）S_△AOB=$\frac{1}{2}$×6×4=12，
设点P的坐标为（x，$\frac{12}{x}$），
由题意得，$\frac{1}{2}$×6×$\frac{12}{x}$=2×12，
解得，x=$\frac{3}{2}$，
则点P的坐标为（$\frac{3}{2}$，8）；
（3）当AC=AB时，点C的坐标为（0，0），
当CA=CB时，点C的坐标为（3，0），
当BA=BC时，作AD⊥OB于D，
由勾股定理得，AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=3$\sqrt{2}$，
∴点C的坐标为（6+3$\sqrt{2}$，0），
综上所述，当△ACB是等腰三角形时，求点C的坐标为（0，0）或（3，0）或（6+3$\sqrt{2}$，0）．

点评 本题考查的是反比例函数的知识、等腰三角形的性质，掌握待定系数法求反比例函数解析式的一般步骤、反比例函数的k的几何意义、灵活运用分情况讨论思想是解题的关键．