题目内容
16. 已知,三角形DEF是三角形ABC的位似三角形(点D,E,F分别对应点A,B,C),原点O为位似中心,三角形DEF与三角形ABC的位似比为k.
已知,三角形DEF是三角形ABC的位似三角形(点D,E,F分别对应点A,B,C),原点O为位似中心,三角形DEF与三角形ABC的位似比为k.(1)若位似比k=$\frac{1}{2}$,请你在平面直角坐标系的第四象限中画出三角形DEF.
(2)若位似比k=n,三角形ABC的面积为S,则三角形DEF的面积=$\frac{S}{{n}^{2}}$.
分析 (1)把点A、B、C的横纵坐标都乘以-$\frac{1}{2}$得到D、E、F的坐标,然后描点即可;
(2)根据相似三角形的性质求解.
解答 解:(1)如图,△DEF为所作;
(2)三角形DEF的面积=$\frac{S}{{n}^{2}}$.
故答案为$\frac{S}{{n}^{2}}$.
点评 本题考查了作图-位似变换:画位似图形的一般步骤为:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.

练习册系列答案
相关题目
6.下列四个有理数中最小的是( )
| A. | 2 | B. | 0 | C. | -5 | D. | 4 |
 小左同学想利用影长测量学校旗杆的高度,如图,她在某一时刻立一长度为1米的标杆,测得其影长为0.8米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.
小左同学想利用影长测量学校旗杆的高度,如图,她在某一时刻立一长度为1米的标杆,测得其影长为0.8米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度. 已知:抛物线C1的顶点坐标为(2,1),且经过(1,0).把C1先向左平移2个单位,再向上平移8个单位得到抛物线C2.
已知:抛物线C1的顶点坐标为(2,1),且经过(1,0).把C1先向左平移2个单位,再向上平移8个单位得到抛物线C2.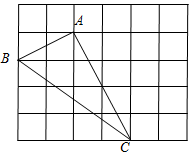 如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识求△ABC的面积.
如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识求△ABC的面积.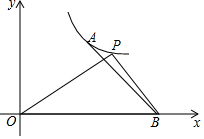 如图,已知反比例函数y=$\frac{k}{x}$(k≠0)图象经过点A(3,4),点B(6,0)在x轴正半轴上.
如图,已知反比例函数y=$\frac{k}{x}$(k≠0)图象经过点A(3,4),点B(6,0)在x轴正半轴上.