题目内容
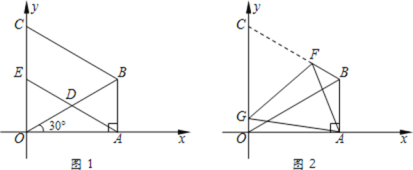
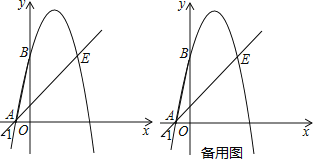
【题目】如图,抛物线y=ax2+4x+c(a≠0)经过点A(﹣1,0),点E(4,5),与y轴交于点B,连接AB.
(1)求该抛物线的解析式;
(2)将△ABO绕点O旋转,点B的对应点为点F.
①当点F落在直线AE上时,求点F的坐标和△ABF的面积;
②当点F到直线AE的距离为![]() 时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.
时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.
【答案】(1)抛物线的解析式是y=﹣x2+4x+5;(2)①当F(﹣4,﹣3)时,S△ABF=6;当F(3,4)时,S△ABF=8;②F点的坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
【解析】(1)将点A、E的坐标代入利用待定系数法进行求解即可得;
(2)①先利用待定系数法求得直线AE的解析式,然后利用旋转的性质求得点F坐标,分情况进行讨论即可得;
②由题意可知直线AE向上平移2个单位或向下平移2个单位,求出平移后的解析式然后分别与二次函数的解析式联立组成方程组进行求解即可得.
(1)将A,E点坐标代入函数解析式,得
![]() ,解得
,解得![]() ,
,
抛物线的解析式是y=﹣x2+4x+5;
(2)①设AE的解析式为y=kx+b,将A,E点坐标代入,得
![]() ,解得
,解得![]() ,
,
AE的解析式为y=x+1,x=0时,y=1,即C(0,1),
设F点坐标为(n,n+1),由旋转的性质得:OF=OB=5,n2+(n+1)2=25,
解得n1=﹣4,n2=3,F(﹣4,﹣3),F(3,4),
当F(﹣4,﹣3)时,如图1,
 ,
,
S△ABF=S△BCF﹣S△ABC=![]() BC|xF|﹣
BC|xF|﹣![]() BC|xA|=
BC|xA|=![]() BC(xA﹣xF),
BC(xA﹣xF),
S△ABF=![]() ×4(﹣1+4)=6;
×4(﹣1+4)=6;
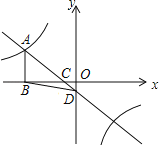
当F(3,4)时,如图2,
 ,
,
S△ABF=S△BCF+S△ABC=![]() BC|xF|+
BC|xF|+![]() BC|xA|=
BC|xA|=![]() BC(xF﹣xA),
BC(xF﹣xA),
S△ABF=![]() ×4(3+1)=8;
×4(3+1)=8;
②如图3,

∵∠HCG=∠ACO,∠HGC=∠COA,∴△HGC∽△COA,
∵OA=OC=1,∴CG=HG=![]() ,由勾股定理,得HC=
,由勾股定理,得HC=![]() =2,
=2,
直线AE向上平移2个单位或向下平移2个单位,
l的解析是为y=x+3,l1的解析是为y=x﹣1,
联立![]() ,
,
解得 ,
, ,
,
![]() ,解得
,解得 ,
, ,
,
F点的坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).

 小学教材全测系列答案
小学教材全测系列答案【题目】甲、乙两名同学进行了6轮投篮比赛,两人的得分情况统计如下:
第1轮 | 第2轮 | 第3轮 | 第4轮 | 第5轮 | 第6轮 | |
甲 | 10 | 14 | 12 | 18 | 16 | 20 |
乙 | 12 | 11 | 9 | 14 | 22 | 16 |
下列说法不正确的是( )
A. 甲得分的极差小于乙得分的极差 B. 甲得分的中位数大于乙得分的中位数
C. 甲得分的平均数大于乙得分的平均数 D. 乙的成绩比甲的成绩稳定