Question

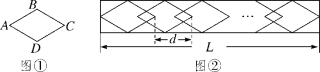
【题目】某工厂沿路护栏的纹饰部分是由若干个和菱形ABCD(如图①)全等的图案组成的，每增加一个菱形，纹饰长度就增加dcm(如图②)．已知菱形ABCD的边长为6cm，∠BAD＝60°.

(1)求AC的长；

(2)若d＝15cm，纹饰总长度L为3918cm，则需要多少个这样的菱形图案？

Answer 1

【答案】（1）AC＝18cm；（2）需要261个这样的菱形图案．

【解析】

（1）连接AC，BD，设交点为O，根据菱形的性质以及勾股定理即可求出AO的长，进而可求出AC的长；

（2）设需要x个这样的图案，仍然根据L=菱形对角线的长+（x-1）d进行计算即可

（1）连接AC，BD，设交点为O，

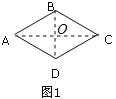
∵四边形ABCD是菱形，∠BAD=60°，

∴∠DAC=30°，

∴OD=AD=3，

∴OA==9，

则AC=2OA=18；

（2）当d=15时，设需x个菱形图案，则有：18+15×（x-1）=3918，

解得x=261，

即需要261个这样的菱形图案．