题目内容
【题目】如图所示,直线AB,CD,EF相交于点O,∠DOB的度数是它余角的2,∠AOE=2∠DOF,OG⊥AB.
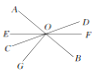
求:(1)∠DOB的度数;
(2)∠BOF的度数;
(3)∠EOG的度数.
【答案】 (1)∠DOB=60°;(2)∠BOF =40°; (3)∠EOG=50°.
【解析】试题分析: (1)首先根据垂直定义可得∠GOB=90°,根据平角定义可得∠COG+∠DOB=90°,再根据∠DOB是它余角的2倍可得![]() ∠DOB+∠DOB=90°,进而可算出∠DOB的度数;
∠DOB+∠DOB=90°,进而可算出∠DOB的度数;
(2)首先根据对顶角相等可得∠AOC的度数,再根据∠AOE=2∠DOF可得3∠COE=60°,继而可得∠COE=20°,∠AOE=40°,由对顶角相等可得∠BOF的度数;
(3)首先计算出∠COG,再计算出∠COE,进而可得答案.
试题解析:
(1)∵∠DOB的度数是它的余角的2倍,
∴∠DOB=2(90°- ∠DOB),
由此得∠DOB=60°.
(2)∵∠AOE=∠BOF,且∠AOE=2∠DOF,
∴∠AOE=∠BOF=![]() ∠DOB=40°.
∠DOB=40°.
(3)∵OG⊥AB,
AOG=90°,
故∠EOG=∠AOG- ∠AOE=90°- 40°=50°.

练习册系列答案
相关题目