题目内容
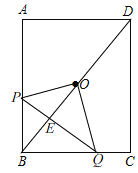
【题目】如图，在矩形ABCD中，AB＝4，BC＝3，点Q在BC上，BQ＝2，点P是AB上的一个动点，连接PQ，将△PBQ沿PQ翻折，点B落在点B′．
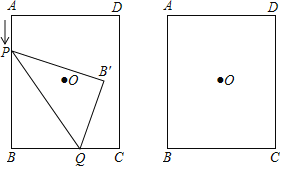
（1）当AP＝ 时，四边形PBQB′的面积是矩形面积的
；
（2）当AP为何值时，四边形PBQB′是正方形？为什么？
（3）在翻折过程中是否存在AP的值，使得点B′与矩形对称中心点O重合，如果存在，请求出AP的值；如果不存在，请说明理由．
【答案】（1）3；（2）当AP为2时，四边形PBQB'是正方形；（3）存在，AP＝4﹣
，
【解析】
（1）先求得矩形ABCD的面积，可知S四边形PBQB'＝6，根据折叠性质可知△PBQ的面积为3，利用三角形面积公式即可解决问题；
（2）利用正方形的性质即可解答；
（3）利用勾股定理求得BD，再利用矩形性质即可知BO，在利用勾股定理求得BE；最后利用相似即可解决问题.
解：（1）在矩形ABCD中，AB＝4，BC＝3，
∴S矩形ABCD＝ABBC＝4×3＝12，
∵四边形PBQB′的面积是矩形面积的
，
∴S四边形PBQB'＝S矩形ABCD＝×12＝6，
由折叠知，△PBQ≌△PB'Q，
∴S△PBQ＝S△PB'Q＝S四边形PBQB'＝3，
∴BQ＝3，
∴S△PBQ＝BQBP＝×2BP＝3，
∴BP＝3，
∴AP＝AB﹣BP＝3，
故答案为：3；
（2）∵四边形PBQB′是正方形，
∴BP＝BQ＝2，
∴AP＝AB﹣BP＝4﹣2＝2，
即：当AP为2时，四边形PBQB'是正方形；
（3）存在，理由：如图，
连接BD，交PQ于E，则BD必过点O，
∵四边形ABCD是矩形，
∴ABC＝∠BAD＝90°，AD＝BC＝3，
根据勾股定理得，BD＝
，
∵O是矩形ABCD的中心，
∴BO＝BD＝×5＝
，
当点B′与矩形对称中心点O重合时，BE＝BO＝
，
由折叠知，BO⊥PQ，
∴∠BEQ＝90°，
在Rt△BEQ中，BQ＝2，
根据勾股定理得，EQ＝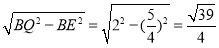
，
∵∠BEQ＝∠PBQ＝90°，∠BQE＝∠PQB，
∴△BEQ∽△PBQ，
∴
，
∴
，
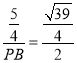∴PB＝ ，
∴AP＝AB﹣PB＝4﹣，
