题目内容
【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．
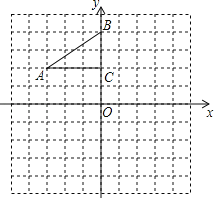
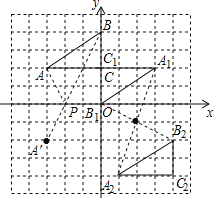
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；平移△ABC，若点A的对应点A2的坐标为（1，﹣4），画出平移后对应的△A2B2C2；
（2）若将△A1B1C绕某一点旋转可以得到△A2B2C2；请直接写出旋转中心的坐标；
（3）在x轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标．
【答案】（1）详见解析；（2）旋转中心为（2，﹣1）；（3）P（﹣2，0）．
【解析】
（1）利用旋转和平移的性质即可完成；
（2）连接旋转前后的对应点即可找出旋转中心；
（3）作点A关于x轴的对称点A′，连接A′B交x轴于点P，则点P即为所求点，利用待定系数法求出直线A′B的解析式为y＝2x+4，再求出其与x轴交点，即为P点坐标.
解：（1）如图所示；
（2）如图，旋转中心为（2，﹣1）；
（3）作点A关于x轴的对称点A′，连接A′B交x轴于点P，则点P即为所求点，
∵A（﹣3，2），
∴A′（﹣3，﹣2）．
设直线A′B的解析式为y＝kx+b（k≠0），
∵A′（﹣3，﹣2），B（0，4），
∴
，
解得
，
∴直线A′B的解析式为y＝2x+4，
∵当y＝0时，x＝﹣2，
∴P（﹣2，0）．
【题目】为弘扬中华传统文化，某校组织八年级800名学生参加汉字听写大赛为了解学生整体听写能力，从中抽取部分学生的成绩（得分取正整数，满分为100分）进行统计分析，得到如下所示的模数分布表：
分数段 | 50.5﹣60.5 | 60.5﹣70.5 | 70.5﹣80.5 | 80.5﹣90.5 | 90.5﹣100.5 |
频数 | 16 | 30 | 50 | m | 24 |
所占百分比 | 8% | 15% | 25% | 40% | n |
请根据尚未完成的表格，解答下列问题：
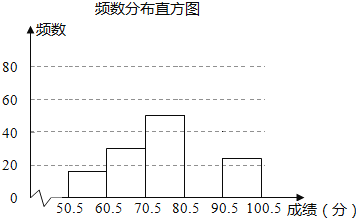
（1）本次抽样调查的样本容量为 ，表中m＝ ．n
（2）补全图中所示的频数分布直方图；
（3）若成绩超过80分为优秀，则该校八年级学生中汉字听写能力优秀的约有多少人？
