题目内容
【题目】在△ABC中，∠C＝90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E.
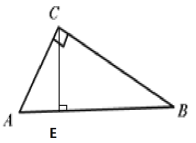
(1)根据已知条件，用尺规作图将图形补充完整，并保留作图痕迹。
(2)求证：△ACD≌△AED；
(3)若∠B＝30°，CD＝1，求BD的长．
【答案】(1)作图见解析；（2）见解析；（3）BD=2.
【解析】
(1)根据题意用尺规作图即可；
（2）根据角平分线性质求出
，根据HL定理求出三角形全等即可；
（3）求出∠DEB=90°，DE=1，根据含30度角的直角三角形性质求出即可．
解：（1）角平分线的作法：
①以A为圆心，AC的长为半径画弧，交AB与点N；
②分别以C、E为圆心，大于
CE为半径画弧，交点为M；
③再连接AM，交CB于点D，AD即为
的角平分线.
再过D点作AB的垂线，交AB于点E，E,N两点重合.
具体作图如下：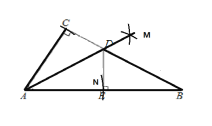
(2)∵AD平分∠CAB，
，
，
∴，
，
∵在
和
中
∴
；
（2）解：∵
，，
∴
，
∵
，
∴由30°的直角三角形中30°所对的直角边是斜边的一半得：
．
练习册系列答案
阅读快车系列答案
相关题目
【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图：
（1）根据图中提供的数据列出如下统计表：
平均成绩（分） | 中位数（分） | 众数（分） | 方差（S2） | |
王华 | 80 | b | 80 | d |
张伟 | a | 85 | c | 260 |
则a= ，b= ，c= ，d= ，
（2）将90分以上（含90分）的成绩视为优秀，则优秀率高的是 ．
（3）现在要从这两个同学选一位去参加数学竞赛，你可以根据以上的数据给老师哪些建议？
