题目内容
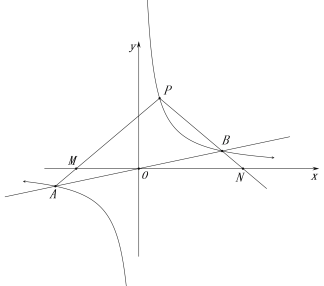
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
(1)求k的值;
(2)设直线PA,PB与x轴分别交于点M,N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P,B之间的动点(与点P,B不重合),连接AQ,BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
【答案】(1)k=4;(2)△PMN是等腰三角形;(3)∠PAQ=∠PBQ,理由见解析.
【解析】
(1)由题意将点B的横坐标代入一次函数![]() 中解得对应的y的值可得点B的坐标,把所得点B的坐标代入
中解得对应的y的值可得点B的坐标,把所得点B的坐标代入![]() 中即可解得k的值;
中即可解得k的值;
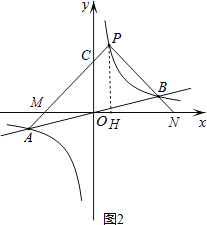
(2)如图2,过点P作PH⊥x轴于H,由k的值得到反比例函数的解析式,由所得反比例函数的解析式和一次函数的解析式可求得点A、B的坐标,这样设点P的坐标为![]() ,由此解得直线PA、PB的解析式,即可求得用含m的代数式表达的点M和N的坐标,从而可求得用m的代数式表达的MH和NH的长度,得到MH=NH,即可得到PH是线段MN的垂直平分线,从而可得PM=PN,由此即可得到△PMN是等腰三角形;
,由此解得直线PA、PB的解析式,即可求得用含m的代数式表达的点M和N的坐标,从而可求得用m的代数式表达的MH和NH的长度,得到MH=NH,即可得到PH是线段MN的垂直平分线,从而可得PM=PN,由此即可得到△PMN是等腰三角形;
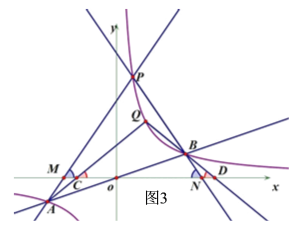
(3)如图3,设QA和x轴相交于点C,QB和x轴相交于点D,则和(2)同理可得QC=QD,由此可得∠QCD=∠QDC,由(2)中所得的PM=PN可得∠PMN=∠PNM,这样结合对顶角相等和三角形外角的性质即可证得∠PAQ=∠PBQ.
(1)把x=4代入![]() ,可得y=1,
,可得y=1,
∴到点B的坐标为(4,1),
把点B(4,1)代入![]() ,得k=4;
,得k=4;
(2)过点P作PH⊥x轴于H,如图2.
由(1)可知反比例函数解析式为:![]() ,
,
由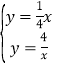 解得:
解得:![]() ,
,![]() ,
,
∴点A的坐标为(-4,-1),点B的坐标为(4,1),
∵点P在![]() 的图象上,
的图象上,
设P的坐标为:![]() ,直线PA的方程为y=ax+b,直线PB的方程为y=px+q,
,直线PA的方程为y=ax+b,直线PB的方程为y=px+q,
把点A、B、P的坐标代入所设解析式可得: 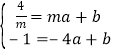 和
和 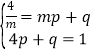 ,
,
由此解得:直线PA的解析式为![]() ,直线PB的解析式为
,直线PB的解析式为![]() ,
,
由此可得:M的坐标为(m-4,0),N的坐标为(m+4,0),
∴H(m,0),
∴MH=m-(m-4)=4,NH=m+4-m=4,
∴MH=NH,
∴PH垂直平分MN,
∴PM=PN,
∴△PMN是等腰三角形;
(3)∠PAQ=∠PBQ.理由如下:
如图3,设QA和x轴相交于点C,QB和x轴相交于点D,则和(2)同理可得QC=QD,
∴∠QCD=∠QDC,
又∵∠QCD=∠MCA,
∴∠MCA=∠QDC,
∵由(2)可知PM=PN,
∴∠PMN=∠PNM,
又∵∠PMN=∠PAQ+∠MCA,∠PNM=∠QDC+∠DBN,
∴∠PAQ+∠MCA=∠QDC+∠DBN,
又∵∠DBN=∠PBQ,
∴∠PAQ+∠MCA=∠QDC+∠PBQ,
∴∠PAQ=∠PBQ.

 阅读快车系列答案
阅读快车系列答案