题目内容
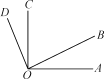
【题目】如图,直线EF、CD相交于点O,OA⊥OB,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
【答案】(1)20°(2)15°(3)∠BOD=![]() ∠AOE,理由见解析。
∠AOE,理由见解析。
【解析】
(1)先求出∠AOF,根据角平分线定义求出∠FOC,根据对顶角相等求出∠EOD=∠FOC,求出∠BOE,即可得出答案;
(2)先求出∠AOF,根据角平分线定义求出∠FOC,根据对顶角相等求出∠EOD=∠FOC,求出∠BOE,即可得出答案;
(3)先求出∠AOF,根据角平分线定义求出∠FOC,根据对顶角相等求出∠EOD=∠FOC,求出∠BOE,即可得出答案.
解:(1)∵∠AOE+∠AOF=180°,∠AOE=40°,
∴∠AOF=140°;
又∵OC平分∠AOF,
∴∠FOC=![]() ∠AOF=70°,
∠AOF=70°,
∴∠EOD=∠FOC=70°;
∵OA⊥OB, ∴∠AOB=90°
∵∠BOE=∠AOB-∠AOE=50°,
∴∠BOD=∠EOD-∠BOE=20°;
(2)∵∠AOE+∠AOF=180°,∠AOE=30°,
∴∠AOF=150°;
又∵OC平分∠AOF,
∴∠FOC=![]() ∠AOF=75°,
∠AOF=75°,
∴∠EOD=∠FOC=75°;
∵∠BOE=∠AOB-∠AOE=60°,
∴∠BOD=∠EOD-∠BOE=15°;
(3)从(1)(2)的结果中能看出∠BOD=![]() ∠AOE,理由如下:
∠AOE,理由如下:
∵∠AOE+∠AOF=180°,
∴∠AOF=180°-∠AOE;
又∵OC平分∠AOF,
∴∠FOC=![]() ∠AOF=90°-
∠AOF=90°-![]() ∠AOE,
∠AOE,
∴∠EOD=∠FOC=90°-![]() ∠AOE;
∠AOE;
∵OA⊥OB, ∴∠AOB=90°
∵∠BOE=∠AOB-∠AOE=90°-∠AOE,
∴∠BOD=∠EOD-∠BOE=(90°-![]() ∠AOE)-(90°-∠AOE)=
∠AOE)-(90°-∠AOE)=![]() ∠AOE;
∠AOE;
∴∠BOD=![]() ∠AOE;
∠AOE;

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案