题目内容
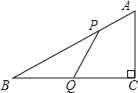
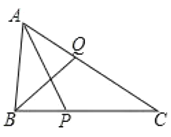
【题目】如图,在△ABC中,∠BAC=60°,∠C=40°,P,Q分别在BC,CA上,AP,BQ分别是∠BAC,∠ABC的角平分线.求证:BQ+AQ=AB+BP.
【答案】证明见解析.
【解析】
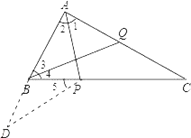
延长AB到D,使BD=BP,连接PD,由题意得:∠D=∠5=∠4=∠C=40°,从而得QB=QC,易证△APD≌△APC,从而得AD=AC,进而即可得到结论.
延长AB到D,使BD=BP,连接PD,则∠D=∠5.
∵AP,BQ分别是∠BAC,∠ABC的平分线,∠BAC=60°,∠ACB=40°,
∴∠1=∠2=30°,∠ABC=180°-60°-40°=80°,∠3=∠4=40°=∠C,
∴QB=QC,
又∠D+∠5=∠3+∠4=80°,
∴∠D=40°.
在△APD与△APC中,

∴△APD≌△APC(AAS),
∴AD=AC.
∴AB+BD=AQ+QC,
∴AB+BP=BQ+AQ.

练习册系列答案
相关题目