题目内容
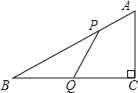
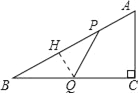
【题目】如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).
(1)若PQ⊥BC,求a的值;
(2)若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.
【答案】(1)![]() (2)点C′不落在线段QB上
(2)点C′不落在线段QB上
【解析】试题分析: (1)∵∠B=∠B,∠PQB=∠C=90°∴△BQP∽△BCA,
∴![]() ,
,![]() ,解得:a=
,解得:a=![]() ,
,
(2) 作QH⊥AB于H,∵PQ=BQ,∴BH=HP,∵∠B=∠B,∠BHQ=∠C,∴△BQH∽△BAC,
∴BH:BC=BQ:AB可得: ![]() (10﹣a):a=8:10,解得a=
(10﹣a):a=8:10,解得a=![]() ,CQ=(8﹣a)=
,CQ=(8﹣a)=![]() ,
,
∴BQ<QC,∴点C′不落在线段QB上.
试题解析:(1)∵∠B=∠B,∠PQB=∠C=90°
∴△BQP∽△BCA,
∴![]() ,
,![]() ,
,
解得:a=![]() ,
,
(2)点C′不落在线段QB上,
作QH⊥AB于H,
∵PQ=BQ,
∴BH=HP,
∵∠B=∠B,∠BHQ=∠C,
∴△BQH∽△BAC,
∴BH:BC=BQ:AB可得: ![]() (10﹣a):a=8:10,
(10﹣a):a=8:10,
解得a=![]() ,
,
CQ=(8﹣a)=![]() ,
,
∴BQ<QC,
∴点C′不落在线段QB上.

【题目】如图,在边长为![]() 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
三角形的直角边长/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
阴影部分的面积/ | 398 | 392 | 382 | 368 | 350 | 302 | 272 | 200 |

(1)在这个变化过程中,自变量、因变量各是什么?
(2)请将上述表格补充完整;
(3)当等腰直角三角形的直角边长由![]() 增加到
增加到![]() 时,阴影部分的面积是怎样变化的?
时,阴影部分的面积是怎样变化的?
(4)设等腰直角三角形的直角边长为![]() ,图中阴影部分的面积为
,图中阴影部分的面积为![]() ,写出
,写出![]() 与
与![]() 的关系式.
的关系式.