题目内容
【题目】在平面直角坐标系![]() 中,对于给定的两点
中,对于给定的两点![]() ,
,![]() ,若存在点
,若存在点![]() ,使得
,使得![]() 的面积等于1,即
的面积等于1,即![]() ,则称点
,则称点![]() 为线段
为线段![]() 的“单位面积点”.
的“单位面积点”.
解答下列问题:
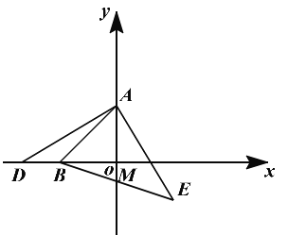
如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() .
.
(1)在点![]() ,
,![]() ,
,![]() ,
,![]() 中,线段
中,线段![]() 的“单位面积点”是______.
的“单位面积点”是______.
(2)已知点![]() ,
,![]() ,点
,点![]() ,
,![]() 是线段
是线段![]() 的两个“单位面积点”,点
的两个“单位面积点”,点![]() 在
在![]() 的延长线上,若
的延长线上,若![]() ,直接写出点
,直接写出点![]() 纵坐标的取值范围.
纵坐标的取值范围.
【答案】(1)A,C;(2)yN1![]() 或yN1+
或yN1+![]() ;yN3
;yN3![]() 或yN3+
或yN3+![]() .
.
【解析】
(1)根据“单位面积点”的定义和点的坐标即可得结果;
(2)根据“单位面积点”的定义,可得点M、N的横坐标,再根据![]() ,即可求得点N的坐标的取值范围.
,即可求得点N的坐标的取值范围.
(1)∵点P的坐标为(1,0),点O的坐标为(0,0),
∴线段OP的“单位面积点”的纵坐标为2或2,
∵点A(1,2),B(1,1),C(1,2),D(2,4),
∴线段OP的“单位面积点”是A. C.
故答案为A,C;
(2)∵点Q(1,2),点P的坐标为(1,0),点M ,N是线段PQ的两个“单位面积点”,
∴点M,点N的横坐标为0或2,
∵点M在HQ的延长线上,
∴点M的横坐标为2,
当x=0时,设点N的坐标为(0,yN),
∵![]() ,
,
∴![]() ×2×|1yN|
×2×|1yN|![]() ,
,
解得yN1![]() 或yN1+
或yN1+![]() ;
;
当x=2时,设点N的坐标为(2,yN),
∵![]() ,
,
∴![]() ×2×|3yN|
×2×|3yN|![]() ,
,
解得yN3![]() 或yN3+
或yN3+![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如图,在边长为![]() 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
三角形的直角边长/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
阴影部分的面积/ | 398 | 392 | 382 | 368 | 350 | 302 | 272 | 200 |

(1)在这个变化过程中,自变量、因变量各是什么?
(2)请将上述表格补充完整;
(3)当等腰直角三角形的直角边长由![]() 增加到
增加到![]() 时,阴影部分的面积是怎样变化的?
时,阴影部分的面积是怎样变化的?
(4)设等腰直角三角形的直角边长为![]() ,图中阴影部分的面积为
,图中阴影部分的面积为![]() ,写出
,写出![]() 与
与![]() 的关系式.
的关系式.
【题目】为落实立德树人根本任务,培养德智体美劳全面发展的社会主义接班人,育才学校在设立学生奖学金时规定:每学期对学生的德智体美劳五个方面进行三次综合素质评价,分别是:假期综合素质评价、期中综合素质评价、期末综合素质评价,八年级(1)班的小明和八年级(2)班的小亮两位同学同时进入一等奖学金测评,他们的三次综合素质评价成绩如下表.
假期综合素质评价成绩 | 期中综合素质评价成绩 | 期末综合素质评价成绩 | |
小明 | 96 | 91 | 92 |
小亮 | 95 | 93 | 91 |
(1)如果从三次综合素质评价成绩稳定性的角度来看,谁可以得一等奖学金?请你通过计算回答;
(2)如果假期综合素质评价成绩、期中综合素质评价成绩、期末综合素质评价成绩按![]() 的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答.
的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答.