Question

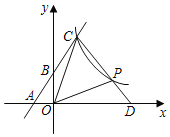
【题目】如图，直线y＝﹣x+4与两坐标轴交于P，Q两点，在线段PQ上有一动点A（点A不与P，Q重合），过点A分别作两坐标轴的垂线，垂足为B，C，则下列说法不正确的是（　　）

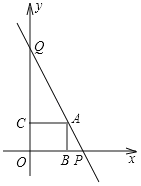
A.点A的坐标为（2，2）时，四边形OBAC为正方形

B.在整个运动过程中，四边形OBAC的周长保持不变

C.四边形OBAC面积的最大值为4

D.当四边形OBAC的面积为3时，点A的坐标为（1，3）

Answer 1

【答案】D

【解析】

根据正方形的判定方法即可判断A，根据一次函数图象上点的坐标特征可设出点A的坐标为（m，﹣m+4），根据矩形的周长公式即可得出C矩形OBA＝8，S矩形OBAC＝OBOC＝m（﹣m+4）＝﹣（m﹣2）2+4，即可判断B、C，由S矩形OBAC＝OBOC＝m（﹣m+4）＝﹣（m﹣2）2+4＝3，求得A的坐标即可判断D．

∵点A分别作两坐标轴的垂线，垂足为B，C，得到矩形OBAC，

当点A的坐标为（2，2）时，则OB＝AB＝2，

∴四边形OBAC为正方形，故A说法正确；

设点A的坐标为（m，﹣m+4）（0＜m＜4），则OB＝m，OC＝﹣m+4，

∴C矩形OBAC＝2（OB+OC）＝2×4＝8，S矩形OBAC＝OBOC＝m（﹣m+4）＝﹣（m﹣2）2+4，

即：四边形OCPD的周长为定值，四边形OBAC面积的最大值为4，故B、C说法正确；

∵当四边形OBAC的面积为3时，则OBOC＝m（﹣m+4）＝3，解得m＝3或1，

∴A为（3，1）或（1，3），故D说法错误，

故选：D．