题目内容
如图,已知⊙O的半径为2,弦AB的长为2| 3 |
 任一点(点C、D均不与A、B重合).
任一点(点C、D均不与A、B重合).(1)求∠ACB;
(2)求△ABD的最大面积.
分析:(1)连接OA、OB,作OE⊥AB,E为垂足,要求∠ACB的度数,根据圆内接四边形的性质只需求得∠ADB的度数,
再根据圆周角定理只需求得圆心角∠AOB的度数,根据等腰三角形的三线合一,只需求得∠AOE的度数,
根据垂径定理求得AE的长,根据锐角三角函数即可由边之间的关系求得∠AOE的度数,进一步求得∠AOB的度数;
(2)要求△ABD的最大面积,由于AB是个定值,只需使AB边上的高最大,即点D是优弧AB的中点,即作DF⊥AB,当DF经过圆心O时,DF取最大值.根据半径和AB的弦心距即可求得.
再根据圆周角定理只需求得圆心角∠AOB的度数,根据等腰三角形的三线合一,只需求得∠AOE的度数,
根据垂径定理求得AE的长,根据锐角三角函数即可由边之间的关系求得∠AOE的度数,进一步求得∠AOB的度数;
(2)要求△ABD的最大面积,由于AB是个定值,只需使AB边上的高最大,即点D是优弧AB的中点,即作DF⊥AB,当DF经过圆心O时,DF取最大值.根据半径和AB的弦心距即可求得.
解答: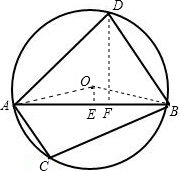 解:(1)连接OA、OB,作OE⊥AB于E,
解:(1)连接OA、OB,作OE⊥AB于E,
∵OA=OB,∴AE=BE,
Rt△AOE中,OA=2,AE=
,
所以sin∠AOE=
,
∴∠AOE=60°,(2分)
∠AOB=2∠AOE=120°,
又∠ADB=
∠AOB,
∴∠ADB=60°,(3分)
又四边形ACBD为圆内接四边形,
∴∠ACB+∠ADB=180°,
从而有∠ACB=180°-∠ADB=120°;(5分)
(2)作DF⊥AB,垂足为F,则:S△ABD=
×2
DF,(6分)
显然,当DF经过圆心O时,DF取最大值,
从而S△ABD取得最大值,
此时DF=DO+OF=2+2sin30°=3,s△ABD=
×6
,
即△ABD的最大面积是3
. (7分)
 解:(1)连接OA、OB,作OE⊥AB于E,
解:(1)连接OA、OB,作OE⊥AB于E,∵OA=OB,∴AE=BE,
Rt△AOE中,OA=2,AE=
| 3 |
所以sin∠AOE=
| ||
| 2 |
∴∠AOE=60°,(2分)
∠AOB=2∠AOE=120°,
又∠ADB=
| 1 |
| 2 |
∴∠ADB=60°,(3分)
又四边形ACBD为圆内接四边形,
∴∠ACB+∠ADB=180°,
从而有∠ACB=180°-∠ADB=120°;(5分)
(2)作DF⊥AB,垂足为F,则:S△ABD=
| 1 |
| 2 |
| 3 |
显然,当DF经过圆心O时,DF取最大值,
从而S△ABD取得最大值,
此时DF=DO+OF=2+2sin30°=3,s△ABD=
| 1 |
| 2 |
| 3 |
即△ABD的最大面积是3
| 3 |
点评:(1)中,主要是能够把已知的线段构造到一个直角三角形中,也可以作直径AM,根据锐角三角函数的知识求得角的度数,再进一步根据圆周角定理和圆内接四边形的性质进行计算;
(2)中,能够分析出面积最大值时,点D的位置.
(2)中,能够分析出面积最大值时,点D的位置.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
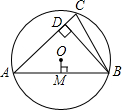 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )| A、0.6 | B、0.8 | C、0.5 | D、1.2 |
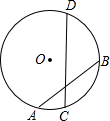 如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )
如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
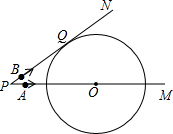 P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.
P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.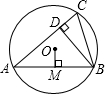 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,作BD⊥AC于点D,OM⊥AB于点M.sin∠CBD=
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,作BD⊥AC于点D,OM⊥AB于点M.sin∠CBD=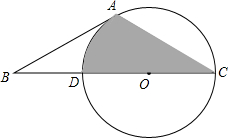 (2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
(2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.