题目内容
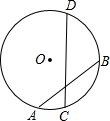 如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )
如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:首先利用相交弦定理求出CE与DE的长,再利用勾股定理求出OF的长,注意计算的正确率.
解答: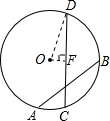 解:作OF⊥CD,垂足为F,
解:作OF⊥CD,垂足为F,
∵两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,
∴AE=BE=4,AE×BE=CE×DE,
假设CE=4x,DE=9x,
∴4×4=4x•9x,
解得:x=
,
∴CE=4×
=
,DE=9×
=6;
∵OF⊥CD,
∴DF=CF=
,⊙O的半径为5,
∴OF=
=
.
故选A.
 解:作OF⊥CD,垂足为F,
解:作OF⊥CD,垂足为F,∵两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,
∴AE=BE=4,AE×BE=CE×DE,
假设CE=4x,DE=9x,
∴4×4=4x•9x,
解得:x=
| 2 |
| 3 |
∴CE=4×
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
∵OF⊥CD,
∴DF=CF=
| 13 |
| 3 |
∴OF=
52- (
|
2
| ||
| 3 |
故选A.
点评:此题主要考查了相交弦定理,垂径定理,勾股定理等知识,题目有一定综合性,是中考中热点问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
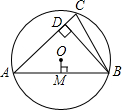 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )| A、0.6 | B、0.8 | C、0.5 | D、1.2 |
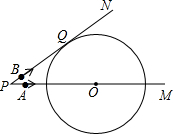 P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.
P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.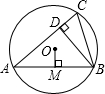 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,作BD⊥AC于点D,OM⊥AB于点M.sin∠CBD=
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,作BD⊥AC于点D,OM⊥AB于点M.sin∠CBD= (2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
(2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.