题目内容
【题目】在平面直角坐标系中，我们定义点P（a，b）的“变换点”为Q．且规定：当a≥b时，Q为（b，﹣a）；当a＜b时，Q为（a，﹣b）．
（1）点（2，1）的变换点坐标为；
（2）若点A（a，﹣2）的变换点在函数y= 
的图象上，求a的值；
（3）已知直线l与坐标轴交于（6，0），（0，3）两点．将直线l上所有点的变换点组成一个新的图形记作M． 判断抛物线y=x2+c与图形M的交点个数，以及相应的c的取值范围，请直接写出结论．
【答案】
（1）（1，﹣2）
（2）
解：当a≥﹣2时，则A（a，﹣2）的变换点坐标为（﹣2，﹣a），
代入y= 
可得﹣a= 
，解得a= 
；
当a＜﹣2时，则A（a，﹣2）的变换点坐标为（a，2），
代入y= 可得2= 
，解得a= ，不符合题意；
综上可知a的值为 ；
（3）
解：设直线l的解析式为y=kx+b （k≠0 ），将点（6，0）、（0，3）代入y=kx+b得： 
，解得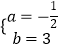 
，
∴直线l的解析式为y=﹣ x+3．
当x=y时，x=﹣ x+3，解得x=2．
点C的坐标为（2，﹣2），点C的变换点的坐标为C′（ 2，﹣2 ），
点（6，0）的变换点的坐标为（0，﹣6），点（0，3）的变换点的坐标为（0，﹣3），
当x≥2时，所有变换点组成的图形是以C′（ 2，﹣2）为端点，过（0，﹣6 ）的一条射线；即：y=2x﹣6，其中x≥2，
当x＜2时，所有变换点组成的图形是以C′（2，﹣2）为端点，过（0，﹣3）的一条射线，即y= x﹣3，其中，x＜2．
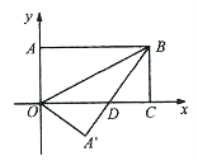
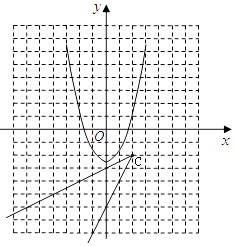
所以新的图形M是以C′（2，﹣2）为端点的两条射线组成的图形．
如图所示：
由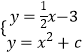 
和 
得：x2﹣ x+c+3=0①和x2﹣2x+c+6=0②
讨论一元二次方程根的判别式及抛物线与点C′的位置关系可得：
①当方程①无实数根时，即：当c＞﹣ 
时，抛物线y=x2+c与图形M没有交点；
②当方程①有两个相等实数根时，即：当c=﹣ 时，抛物线y=x2+c与图形M有一个交点；
③当方程②无实数根，且方程①有两个不相等的实数根时，即：当﹣5＜c＜﹣ 时，抛物线y=x2+c与图形M有两个交点；
④当方程②有两个相等实数根或y=x2+c恰好经过经过点C′时，即：当c=﹣5或c=﹣6时，抛物线y=x2+c与图形M有三个交点；
⑤当方程②方程①均有两个不相等的实数根时，且两根均小于2，即：当﹣6＜c＜﹣5时，抛物线y=x2+c与图形M有四个交点；
⑥当c＜﹣6时，抛物线y=x2+c与图形M有两个交点．
【解析】解：（1）∵2≥﹣1，
∴点（2，1）的变换点坐标为（1，﹣2），
所以答案是：（1，﹣2）；
【考点精析】关于本题考查的二次函数的性质，需要了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．
