题目内容
【题目】在平面直角坐标系中，正方形
的点
，
，
，现将此正方形绕
逆时针旋转
，得到正方形
，求正方形各顶点的坐标．
【答案】
，
，
，
．
【解析】
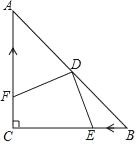
作A1D⊥x轴于D，C1E⊥x轴于E，如图，根据正方形的性质得OB=2
，∠BOA=∠BOC=45°，再根据旋转的性质得点B1在y轴上，OB1=OB=2，∠A1OD=45°，∠B1OC1=45°，OA1=OA=OC1=2，则可判断△A1OD和△EOC1都是等腰直角三角形，于是可根据等腰直角三角形的性质得到A1D=OD=
OA1=，C1E=OE=OC1=，然后根据各象限点的坐标特征和y轴上点的坐标特征写出正方形OA1B1C1各顶点的坐标．
解：作
轴于
，
轴于
，如图，
∵正方形
的点
，，
，
∴
，
，
∴正方形绕
逆时针旋转
，得到正方形
，
∴点
在
轴上，
，
，
，
，
∴
和
都是等腰直角三角形，
∴
，
，
∴，，，．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
