��Ŀ����
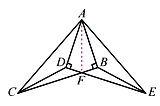
����Ŀ����ͼ������ABC�У���C=90�㣬AC=BC=4cm����D��б��AB���е㣬��E�ӵ�B������1cm/s���ٶ����C�˶�����Fͬʱ�ӵ�C������һ�����ٶ�������CA�����˶����涨������E���յ�Cʱֹͣ�˶������˶���ʱ��Ϊx�룬����DE��DF��
��1����գ�S��ABC=�� ��cm2��
��2����x=1�ҵ�F�˶����ٶ�Ҳ��1cm/sʱ����֤��DE=DF��
��3��������F��3cm/s���ٶ�������CA�����˶����ڵ�E����F�˶������У������ij��ʱ��x��ʹ����ADF���������BDE���������������ϵ������ֱ��д��ʱ��x��ֵ��

���𰸡���1��8��2��֤����������3��![]() ��4��
��4��![]() ��
��![]()
��������
��1��ֱ�ӿ����ABC���������2������CD�����ݵ���ֱ�������ε����ʿ���A=��B=��ACD=��DCB=45�㣬��BD=CD����BE=CF������֤��CDF�ա�BDE���ɵ�DE=DF��
��3���֡�ADF������ǡ�BDE������������͡�BDE���ADF�������2������������ۣ����������г����̿���x��ֵ��
��1����S��ABC=![]() AC��BC
AC��BC
��S��ABC=![]() ��4��4=8��cm2��
��4��4=8��cm2��
�ʴ�Ϊ��8
��2����ͼ������CD
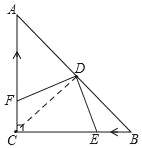
��AC=BC��D��AB�е�
��CDƽ����ACB
���ߡ�ACB=90��
���A=��B=��ACD=��DCB=45��
��CD=BD
������ã�BE=CF
������CDF����BDE��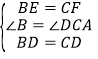 ,
,
���CDF�ա�BDE��SAS��
��DE=DF
��3����ͼ������D��DM��BC�ڵ�M��DN��AC�ڵ�N��
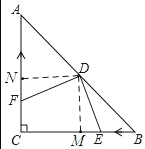
��AD=BD����A=��B=45�㣬��AND=��DMB=90��
���ADN�ա�BDM��AAS��
��DN=DM
��S��ADF=2S��BDE��
��![]() ��AF��DN=2��
��AF��DN=2��![]() ��BE��DM
��BE��DM
��|4��3x|=2x
��x1=4��x2=![]()
��2S��ADF=S��BDE
��2��![]() ��AF��DN=
��AF��DN=![]() ��BE��DM
��BE��DM
��2��|4��3x|=x
��x1=![]() ��x2=
��x2=![]()
����������x=![]() ��4��
��4��![]() ��
��![]() .
.

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�