题目内容
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A. 点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动_________秒后,△AMN是等边三角形?
(2)点M、N在BC边上运动时,运动_______秒后得到以MN为底边的等腰三角形△AMN?
(3)M、N同时运动几秒后,△AMN是直角三角形?请说明理由.

【答案】(1)4;(2)16;(3)M、N同时运动3,![]() ,15,18秒后,△AMN是直角三角形,理由见解析.
,15,18秒后,△AMN是直角三角形,理由见解析.
【解析】
(1)根据题意设点M、N运动t秒后,可得到等边三角形△AMN,然后表示出AM,AN的长,由于∠A等于60°,所以只要AM=AN三角形ANM就是等边三角形;
(2)由△AMN是等腰三角形,可证出△ACM≌△ABN,可得CM=BN,设出运动时间,表示出CM,NB,NM的长,列出方程,可解出未知数的值;
(3)分点N在AB,AC,BC上运动的三种情况,再分别就∠AMN=90°和∠ANM=90°列方程求解可得.
解:(1)设点M、N运动t秒后,可得到等边三角形△AMN,如图1,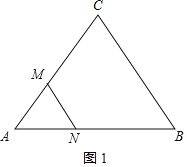
AM=t,AN=12-2t,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠A=60°,
当AM=AN时,△AMN是等边三角形
∴t=12-2t,
解得t=4,
∴点M、N运动4秒后,△AMN是等边三角形;
(2)设当点M、N在BC边上运动时,运动t秒后得到以MN为底边的等腰三角形△AMN,
由题意知12秒时M、N两点重合,恰好在C处,
如图2,假设△AMN是等腰三角形,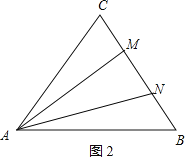
∴AM=AN,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
∵∠AMC =∠ANB,∠C=∠B,AC=AB
∴△ACM≌△ABN(AAS),
∴CM=BN,
∴t-12=36-2t,
解得t=16,符合题意.
所以点M、N在BC边上运动时,运动16秒后能得到以MN为底的等腰三角形;
(3)①当点N在AB上运动时,如图3,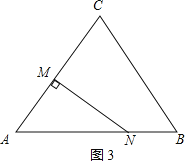
若∠AMN=90°,∵BN=2t,AM=t,
∴AN=12-2t,
∵∠A=60°,
∴2AM=AN,即2t=12-2t,
解得t=3;
如图4,若∠ANM=90°,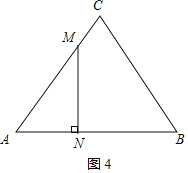
由2AN=AM得2(12-2t)=t,
解得t=![]() ;
;
②当点N在AC上运动时,点M也在AC上,此时A,M,N不能构成三角形;
③当点N在BC上运动时,如图5,
当点N位于BC中点处时,由△ABC时等边三角形知AN⊥BC,即△AMN是直角三角形,
则2t-24=6,
解得t=15;
如图6,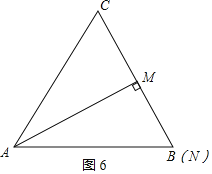
当点M位于BC中点处时,由△ABC时等边三角形知AM⊥BC,即△AMN是直角三角形,
则t-12=6
解得t=18;
综上, M、N同时运动3,![]() ,15,18秒后,△AMN是直角三角形;
,15,18秒后,△AMN是直角三角形;
故答案为:3,![]() ,15,18.
,15,18.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案