题目内容
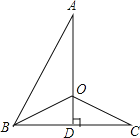
【题目】如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠AOC=130°,则∠ABC= .
【答案】80°
【解析】
试题分析:由题意得到OD垂直平分BC,利用线段垂直平分线定理得到BO=CO,利用三线合一得到OD为角平分线,由∠AOC度数,利用邻补角定义求出∠BOD度数,进而求出∠OBD度数,再由BO为角平分线求出∠ABC度数即可.
解:∵AD⊥BC,D为BC的中点,
∴OD垂直平分BC,即BD=CD,
∴OB=OC,∠BOD=∠COD,
∵∠AOC=130°,
∴∠BOD=∠COD=50°,
在Rt△BOD中,∠OBD=40°,
∵BO平分∠ABC,
∴∠ABO=∠OBD,
则∠ABC=2∠OBD=80°,
故答案为:80°

练习册系列答案
相关题目