题目内容
【题目】如图，在△ABC中，∠C=90°，AC=6，BC=8.
（1）用直尺和圆规作∠A的平分线，交BC于点D；（要求：不写作法，保留作图痕迹）
（2）求S△ADC: S△ADB的值.
【答案】（1）见解析；（2）
.
【解析】
（1）以A为圆心,以任意长度为半径作弧,分别交AC、AB于P、Q，分别以P、Q为圆心，以大于
PQ长度为半径作弧，交于点M，连接AM并延长，交BC于D，从而作出AD；
（2）过点D作DE⊥AB于E，根据勾股定理求出AB，然后根据角平分线的性质可得：DE=DC，最后根据三角形的面积公式求S△ADC: S△ADB的比值即可.
解:（1）以A为圆心,以任意长度为半径作弧,分别交AC、AB于P、Q，分别以P、Q为圆心，以大于PQ长度为半径作弧，交于点M，连接AM并延长，交BC于D，如图所示：AD即为所求；
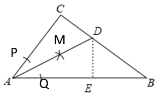
（2）过点D作DE⊥AB于E
∵AC=6，BC=8
根据勾股定理可得：AB=
∵AD平分∠CAB，DC⊥AC
∴DE=DC
∴S△ADC: S△ADB=（AC·DC）：（AB·DE）= AC：AB=6:10=
练习册系列答案
名校课堂系列答案
相关题目
