Question

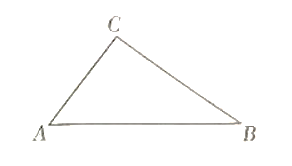
【题目】如图，等边三角形的边长为，点为上的一点，点为上的一点，连结、，．

求证：①；②；

若，求和的长．

Answer 1

【答案】（1）证明见解析；（2）CD=．

【解析】

（1）①由△ABC为等边三角形，易得∠B=∠C=60°，又∠APD=60°，由外角性质可得∠DPC=∠PAB，利用相似三角形的判定定理（AA）可得△ABP∽△PCD；

②由∠PAC=∠DAP，∠C=∠APD=60°，由相似三角形的判定定理（AA定理）可得△ADP∽△APC，利用相似三角形的性质可得结论；

（2）由AB=BC=3，PC=2，得到BP=1，由△ABP∽△PCD，利用相似三角形的性质可得，易得CD，可得AD，再利用AP2=ADAC，可得AP．

（1）①在等边三角形△ACB中，∠B=∠C=60°．

∵∠APD=60°，∠APC=∠PAB+∠B，∴∠DPC=∠PAB，∴△ABP∽△PCD；

②∵∠PAC=∠DAP，∠C=∠APD=60°，∴△ADP∽△APC，∴，∴AP2=ADAC；

（2）∵AB=BC=3，PC=2，∴BP=1．

∵△ABP∽△PCD，∴，∴CD==，∴AD=3﹣=．

∵AC=3，AD=，AP2=ADAC，∴AP=．