题目内容
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上, OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当 时,
时,  的值为 ;当
的值为 ;当 时,
时, 为 .(用含n的式子表示)
为 .(用含n的式子表示)
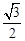 ;
; .
.
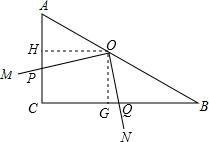
解析试题分析:如图,过点O作OH⊥AC于H,OG⊥BC于G,∴∠OHP=∠OGQ=90°.
∵∠ACB=90°,∴四边形HCGO为矩形. ∴∠HOG=90°.∴∠HOP=∠GOQ. ∴△PHO∽△QGO.∴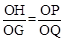 .
.
又∵△AHO∽△OGB,∴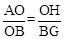 .
.
当 时 ,由∠ABC=30°,设AH=x,则OA=2x,OH=
时 ,由∠ABC=30°,设AH=x,则OA=2x,OH=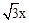 ,OB="4x,OG=2x," ∴
,OB="4x,OG=2x," ∴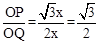 .
.
当 时 ,由∠ABC=30°,设AH=x,则OA=2x,OH=
时 ,由∠ABC=30°,设AH=x,则OA=2x,OH=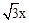 ,OB="4nx,OG=2nx," ∴
,OB="4nx,OG=2nx," ∴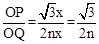 .
.
考点:1.相似三角形的判定和性质;2.含30度角的直角三角形;3.旋转的性质.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目

 ,
, 是斜边AB的中点,过
是斜边AB的中点,过 于
于 ,连结
,连结 交
交 于
于 ;过
;过 于
于 ,连结
,连结 交
交 ;过
;过 于
于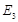 ,…,如此继续,可以依次得到点
,…,如此继续,可以依次得到点 ,
,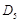 …,
…, ,分别记
,分别记 ,
, ,
, ,…,
,…, 的面积为
的面积为 ,
, ,
, ,…
,… ,则
,则 .
.



 ,则在这两个三角形中,面积较小的三角形与面积较大的三角形的周长之比为 .
,则在这两个三角形中,面积较小的三角形与面积较大的三角形的周长之比为 . 三个顶点的坐标分别为
三个顶点的坐标分别为 ,以原点为位似中心,将△
,以原点为位似中心,将△ 缩小,位似比为
缩小,位似比为 ,则线段
,则线段 的中点
的中点 变换后对应点的坐标为_________.
变换后对应点的坐标为_________. 