题目内容
如图,点A1、A2、A3、…,点B1、B2、B3、…,分别在射线OM、ON上,A1B1∥A2B2∥A3B3∥A4B4∥….如果A1B1=2,A1A2=2OA1,A2A3=3OA1,A3A4=4OA1,….那么A2B2= ,AnBn= .(n为正整数)
6;n(n+1).
解析试题分析:根据OA1=1,求出A1A2、A2A3、A3A4的值,推出AnAn-1的值,根据平行线分线段成比例定理得出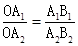 ,代入求出A2B2=6=2×(2+1),A3B3=12=3×(3+1),A4B4=20=4(4+1),推出AnBn=n(n+1)即可:∵OA1=1,
,代入求出A2B2=6=2×(2+1),A3B3=12=3×(3+1),A4B4=20=4(4+1),推出AnBn=n(n+1)即可:∵OA1=1,
∴A1A2=2×1=2,
A2A3=3×1=3,
A3A4=4,
…
An-2An-1=n-1,
An-1An=n,
∵A1B1∥A2B2∥A3B3∥A4B4∥…,
∴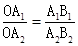 ,
,
∴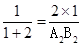 ,
,
∴A2B2=6=2×(2+1),
A3B3=12=3×(3+1),
A4B4=20=4(4+1),
…
∴AnBn=n(n+1),
故答案为:6,n(n+1).
考点:平行线分线段成比例.

练习册系列答案
相关题目

 、
、 两点分别在
两点分别在 的边
的边 、
、 上,
上, 与
与 不平行,当满足条件(写出一个即可) 时,
不平行,当满足条件(写出一个即可) 时, ∽
∽ .
.
 .
. 时,
时,  的值为 ;当
的值为 ;当 时,
时,



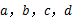 是成比例线段,即
是成比例线段,即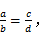 其中
其中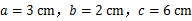 ,则
,则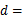 ______
______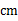 .
.