题目内容
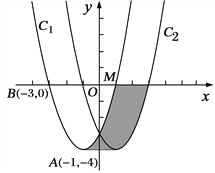
【题目】如图,在平面直角坐标xOy中,抛物线![]() 的顶点为A(-1,-4),且过点B(-3,0)
的顶点为A(-1,-4),且过点B(-3,0)
(1)将抛物线![]() 向右平移2个单位得抛物线
向右平移2个单位得抛物线![]() ,设C2的解析式为y=ax2+bx+c,求a,b,c的值;
,设C2的解析式为y=ax2+bx+c,求a,b,c的值;
(2)在(1)的条件下,直接写出ax2+bx+c>5的解集_________________
(3)写出阴影部分的面积![]() =_____________.
=_____________.
【答案】(1)a,b,c的值分别为1,-2,-3;(2)x<-2或x>4;(3)8.
【解析】(1)设抛物线C1的解析式为y=a(x+1)2-4,将B点代入解析式,求a,再由平移的规律得出C2的解析式,从而得出a,b,c的值;
(2)令y=5,得出x的值,根据图象得出ax2+bx+c>5的解集.
(3)阴影部分可以转换成求平行四边形的面积,即函数图象平移的距离乘以A点纵坐标的绝对值.
(1)设抛物线C1的解析式为y=a(x+1)2-4,
将点B(-3,0)代入得a=1,
∴抛物线的解析式为y=(x+1)2-4,
∵将抛物线C1向右平移2个单位得抛物线C2,
∴抛物线C2的解析式为y=(x-1)2-4,
∴a,b,c的值分别为1,-2,-3;
(2)令y=(x-1)2-4中y=5,得x=4或-2.
∴x<-2或x>4时,ax2+bx+c>5,
即ax2+bx+c>5的解集为x<-2或x>4;
(3)阴影部分可以转换成求平行四边形的面积,S=2×|yA|=2×4=8,

练习册系列答案
相关题目