题目内容
【题目】如图 1，△AOB中，∠AOB＝90°，OA＝OB，A(3，2)，AB交 x轴于 C点
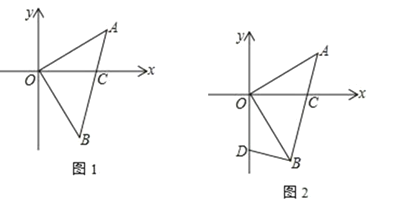
(1) 求△AOB的面积
(2) 如图2，点 D(0，
)在 y轴上，连 BD，求证：BD⊥AB
【答案】（1）
（2）见解析
【解析】
（1）根据题意可知△ABC为等腰直角三角形，故求出AO的长，即可求出面积；
（2）根据S△AOB=S△AOC+S△BOC，由OC为底，△AOC与△BOC以OC为底的高之和为5，可求出OC的长，得到OD=OC，再证明△AOC≌△BOD，即可证明BD⊥AB
（1）∵∠AOB＝90°，OA＝OB，
∴△ABC为等腰直角三角形，
∵A(3，2)，
∴OA=
=OB
∴S△AOB=
（2）∵S△AOB=S△AOC+S△BOC=
∵△AOC与△BOC以OC为底的高之和为5，
∴S△AOB=
故OC=
，
∵D(0，
)
∴OD=OC，
∵∠AOB＝90°，
∴∠AOC+∠BOC=∠BOD+∠BOC，
∴∠AOC=∠BOD
又OA＝OB，
∴△AOC≌△BOD，
∴∠DBC=∠DBO+∠OBC=∠CAO+∠OBC=90°，
∴BD⊥AB
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
