Question

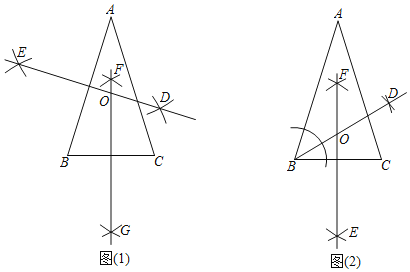
【题目】如图，已知在平行四边形ABCD中，AE⊥BC，垂足为E，CE=AB，点F为CE的中点，点G在线段CD上，联结DF，交AG于点M，交EG于点N，且∠DFC=∠EGC．

（1）求证：CG=DG；

（2）求证：．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）首先证明△ECG≌△DCF，则有CG=CF，因为CF=CE，则有CG=CD，则结论可证；

（2）延长AG、BC交于点H，首先证明△ADG≌△HCG，则有AG=HG，然后根据直角三角形斜边中线有AG=HG=EG，进而得出∠CDF=∠DAH，进一步可证△ADG∽△DMG，则有，即，又因为CG=DG即可证明结论．

证明：（1）∵四边形ABCD是平行四边形，CE=AB，

∴AB=CD=EC．

又∵∠DFC=∠EGC，∠FCD=∠GCE，

∴△ECG≌△DCF，

∴CG=CF．

∵点F为CE的中点，

∴CF=CE，

∴CG=CD，

即：CG=DG．

（2）延长AG、BC交于点H．

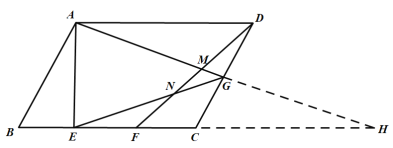
∵△ECG≌△DCF，

∴∠CEG=∠CDF，DG=CG．

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠DAH=∠H，∠ADC=∠DCH．

∴△ADG≌△HCG，

∴AG=HG．

∵AE⊥BC，

∴∠AEC=90°，

∴AG=HG=EG．

∴∠CEG=∠H，

∴∠CDF=∠DAH．

又∵∠AGD=∠DGM，

∴△ADG∽△DMG．

∴，

∴

又∵CG=DG，

∴．