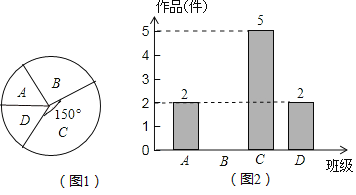
题目内容
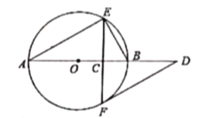
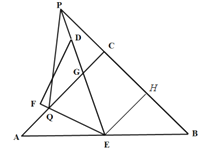
【题目】如图,△ABC和△DEF都是等腰直角三角形,∠ACB=∠EFD=90,△DEF,的顶点E与△ABC的斜边AB的中点重合.将△DEF绕点E旋转,旋转过程中,线段AC与线段EF相交于点Q,射线ED与射线BC相交于点P.
(1)求证:△AEQ∽△BPE;
(2)求证:PE平分∠BPQ;
(3)当AQ=2,AE=![]() ,求PQ的长.
,求PQ的长.

【答案】(1)证明见解析;(2)证明见解析;(3)5
【解析】
(1)求出∠A=∠B=∠DEF=45和∠AEQ=∠BPE ,即可证明相似.
(2)证明△AEQ∽△EPQ,推出∠EPQ=∠BPE即可解答.
(3) 过点E作EH⊥BP于点H, 根据条件求出△AEQ∽△BPE,推出PE,再利用相似解答.
解:(1)证明:∵△ABC和△DEF都是等腰直角三角形,
∴∠A=∠B=∠DEF=45,
而∠PEB+∠AEQ=∠PEB+∠EPB=180-45=135
∴∠AEQ=∠BPE
∴△AEQ∽△BPE;
(2)∵△AEQ∽△BPE,∴∠AEQ=∠BPE,![]() ,
,
而AE=BE,∴![]() ,…
,…
∵∠A=∠DEF=45,
∴△AEQ∽△EPQ,
∴∠AEQ=∠EPQ,∴∠EPQ=∠BPE,
即PE平分∠BPQ;
(3)过点E作EH⊥BP于点H,AQ=2,AE=![]()
∵AE=BE=![]() ,∠ACB=90,AC=BC,由勾股定理易得AC=BC=6,
,∠ACB=90,AC=BC,由勾股定理易得AC=BC=6,
∵∠B=45,BE=![]() ,易得EH=BH=3
,易得EH=BH=3
∵△AEQ∽△BPE,∴![]() , ∴
, ∴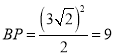 …
…
∴PH=BP-BH=9-3=6, ∴![]() …
…
∵△AEQ∽△EPQ∽△BPE,
∴![]() ,∴
,∴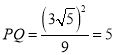 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目