Question

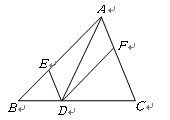
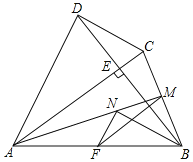
【题目】如图，四边形ABCD中，AC⊥BD交BD于点E，点F、M分别是AB、BC的中点，BN平分∠ABE交AM于点N，AB＝AC＝BD，连接MF，NF

求证：（1）BN＝MN；

（2）△MFN∽△BDC．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）根据等腰三角形的性质，可得是高线、顶角的角平分线，根据直角三角形的性质，可得，根据三角形外角的性质，可得，进而可知是等腰直角三角形，即得．

（2）根据三角形中位线的性质，可得与的关系，根据等量代换，可得与的关系，根据等腰直角三角形，可得与的关系，根据等量代换，可得与的关系，根据同角的余角相等，可得与的关系，根据两边对应成比例且夹角相等的两个三角形相似，可得答案．

（1）证明：∵，点是的中点

∴，平分

∵平分

∴

∵

∴

∴

∴

∴是等腰直角三角形

∴

（2）证明：∵点，分别是，的中点，

∴，

∵

∴，即

∵是等腰直角三角形

∴，即

∴

∵

∴

∵

∴

∵

∴

∴

∴

∴