题目内容
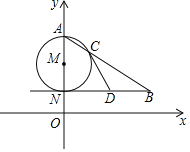
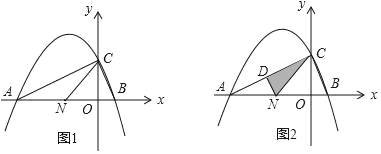
【题目】如图1,抛物线y=﹣![]() x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣
x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣![]() ,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:
,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:
(1)求出抛物线的解析式,并写出C点的坐标;
(2)试求出当n为何值时,△ANC恰能构成是等腰三角形.
(3)如图2,过N作NF∥BC,与AC相交于D点,连结CN,请问在N点的运动过程中,△CDN的面积是否存在最大值;若存在,试求出该最大面积,若不存在,请说明理由.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+2,C(0,2);(2)当n=2
x+2,C(0,2);(2)当n=2![]() ﹣4或﹣
﹣4或﹣![]() 时,△ANC是等腰三角形;(3)当n=﹣
时,△ANC是等腰三角形;(3)当n=﹣![]() 时,△DCN的面积最大,最大值为
时,△DCN的面积最大,最大值为![]() .
.
【解析】
(1)由抛物线y=﹣![]() x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,不妨设抛物线的解析式为y=﹣
x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,不妨设抛物线的解析式为y=﹣![]() (x+4)(x﹣1),由此即可解决问题;
(x+4)(x﹣1),由此即可解决问题;
(2)分别表示出AC、AN、NC,然后分三种情形讨论:①当AN=AC时;②当NA=NC时,③当NC=AC时;分别构建方程即可解决问题;
(3)根据S△CDN=S△ANC﹣S△ADN构建二次函数,利用二次函数的性质解决最值问题;
(1)∵抛物线y=﹣![]() x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,不妨设抛物线的解析式为y=﹣
x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,不妨设抛物线的解析式为y=﹣![]() (x+4)(x﹣1),即y=﹣
(x+4)(x﹣1),即y=﹣![]() x2﹣
x2﹣![]() x+2,∴C(0,2).
x+2,∴C(0,2).
(2)∵A(﹣4,0),N(n,0),C(0,2),∴AC=![]() =2
=2![]() ,AN= n+4,NC=
,AN= n+4,NC=![]() .
.
分三种情况讨论:
①当AN=AC时,n+4=2![]() ,解得:n=2
,解得:n=2![]() ﹣4.
﹣4.
②当NA=NC时,n+4=![]() ,解得:n=﹣
,解得:n=﹣![]() .
.
③当NC=AC时,![]() =2
=2![]() ,解得:n=±4.
,解得:n=±4.
∵点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),故这种情况不成立.
综上所述:当n=2![]() ﹣4或﹣
﹣4或﹣![]() 时,△ANC是等腰三角形.
时,△ANC是等腰三角形.
(3)由题意可知:直线BC的解析式为y=﹣2x+2,直线AC的解析式为y=![]() x+2,设N(n,0).
x+2,设N(n,0).
∵ND∥BC,设ND的解析式为y=﹣2x+b,代入(n,0)可得:b=2n,∴ND的解析式为y=﹣2x+2n,由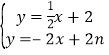 ,可得点D的纵坐标:yD=
,可得点D的纵坐标:yD=![]() (8+2n),∴S△CDN=S△ANC﹣S△ADN =
(8+2n),∴S△CDN=S△ANC﹣S△ADN =![]() [2×(n+4)﹣
[2×(n+4)﹣![]() (8+2n)(n+4)]=
(8+2n)(n+4)]=![]() =﹣
=﹣![]() (n+
(n+![]() )2+
)2+![]() .
.
∵﹣![]() <0,∴当n=﹣
<0,∴当n=﹣![]() 时,△DCN的面积最大,最大值为
时,△DCN的面积最大,最大值为![]() .
.