题目内容
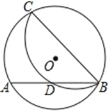
【题目】如图，在△ABC中，AB＝3，D是AB上的一点（不与点A、B重合），DE∥BC，交AC于点E，则
的最大值为_____．
【答案】
【解析】
设AD＝x，
＝y，由△ADE∽△ABC知
＝
x2①，又CE=AC-AE，故
＝
，由△ADE的边AE上的高和△CED的边CE上的高相等，得
＝
＝②，由①②得y＝＝－x2＋
x，再根据0＜x＜3即可求出最大值．
设AD＝x，＝y ，
∵AB＝3，AD＝x，
∴＝
＝
，
∴＝x2①，
∵DE∥BC，
∴△ADE∽△ABC，
∴
＝
，
∵AB＝3，AD＝x，
∴＝
，
∴＝
，
∵△ADE的边AE上的高和△CED的边CE上的高相等，
∴＝＝②，
①÷②，得
∴y＝
＝－x2＋x，
∵AB＝3，
∴x的取值范围是0＜x＜3；
∴y＝＝－(x－
)2＋≤，
∴的最大值为．
故答案为．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
