题目内容
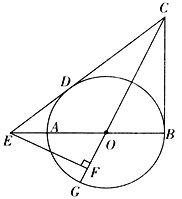
【题目】如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F。
(1)求证:∠FEB=∠ECF
(2)BC= 12, DE=8 求 EA的长。
【答案】(1)详见解析;(2)4.
【解析】
(1)利用切线长定理得到OC平分∠BCE,即∠ECF=∠BCO,利用切线的性质得OB⊥BC,则∠BCO+∠COB=90°,由于∠FEB+∠FOE=90°,∠COB=∠FOE,所以∠FEB=∠ECF;
(2)连接OD,如图,利用切线长定理和切线的性质得到CD=CB=12,OD⊥CE,则CE=20,利用勾股定理可计算出BE=16,设⊙O的半径为r,则OD=OB=r,OE=16﹣r.在Rt△ODE中,根据勾股定理得r2+82=(16﹣r)2,解得r=6,即可得出EA的长.
(1)∵CB、CD分别切⊙O于点B,D,∴OB![]() BC,OC平分∠BCE,即∠ECF=∠BCO.
BC,OC平分∠BCE,即∠ECF=∠BCO.
∵∠OBC=90°,∴∠BCO+∠COB=90°.
∵EF![]() OG,∴∠FEB+∠FOE=90°.
OG,∴∠FEB+∠FOE=90°.
又∵∠COB=∠FOE,∴∠FEB=∠BCO=∠ECF.
(2) 连接OD.
∵CB、CD分别切⊙O于点B,D,∴ CD=CB=12,OD![]() CE,∴CE=CD+DE=12+8=20.
CE,∴CE=CD+DE=12+8=20.
在Rt△BCE中,![]()
设⊙O的半径为r,则OD=OB=r,OE=16-r.
在Rt△ODE中,![]() ,解得:r=6.
,解得:r=6.
∴EA=EB一2r=16 一12= 4.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目