题目内容
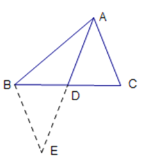
【题目】仔细阅读下面的解题过程,并完成填空:如图13,AD为△ABC的中线,已知AD=4cm,试确定AB+AC的取值范围.
解:延长AD到E,使DE = AD,连接BE.
因为AD为△ABC的中线,
所以BD=CD.
在△ACD和△EBD中,因为AD=DE,∠ADC=∠EDB,CD=BD,所以△ACD≌△EBD(__________).
所以BE=AC(_____________________).
因为AB+BE>AE(_____________________),
所以AB+AC>AE.
因为AE=2AD=8cm,
所以AB+AC>_______cm.
【答案】答案见解析
【解析】
根据三角形全等的判定与性质以及三角形的内角和,即可得出答案.
解:延长AD到E,使DE = AD,连接BE.
因为AD为△ABC的中线,
所以BD=CD.
在△ACD和△EBD中,因为AD=DE,∠ADC=∠EDB,CD=BD,所以△ACD≌△EBD(SAS).
所以BE=AC(全等三角形的性质).
因为AB+BE>AE(两边之和大于第三边),
所以AB+AC>AE.
因为AE=2AD=8cm,
所以AB+AC>8cm.

练习册系列答案
相关题目