Question

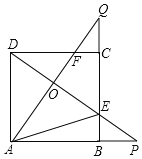
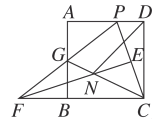
【题目】(1)如图，正方形ABCD中，∠PCG＝45°，且PD＝BG，求证：FP＝FC.

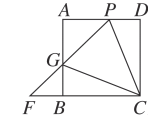
(2)如图，正方形ABCD中，∠PCG＝45°，延长PG交CB的延长线于点F，(1)中的结论还成立吗？请说明理由．

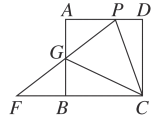
(3)在(2)的条件下，作FE⊥PC，垂足为E，交CG于点N，连接DN，求∠NDC的度数．

Answer 1

【答案】(1)见解析；　(2)成立，理由见解析；(3)∠NDC＝45°.

【解析】

（1）根据已知条件易证△BCG≌△DCP，由全等三角形的性质可得CP=CG，∠BCG=∠DCP，即可求得∠DCP=∠BCG=22.5°，所以∠PCF=∠PCG+∠BCG=67.5°；在△PCG中，根据等腰三角形的性质及三角形的内角和定理求得∠CPG=67.5°，即可得∠CPG =∠PCF，由此证得PF=CF；（2）过点C作CH⊥CG交AD的延长线于H，先证得△BCG≌△DCH，可得CG=CH，再证得∠PCH=45°=∠PCG，利用SAS证明△PCH≌△PCG，即可得∠CPG=∠CPH，再利用等角的余角相等证得∠CPF=∠PCF，由此即可证得PF=CF；（3）连接PN，由（2）知PF=CF，已知EF⊥CP，由等腰三角形的三线合一的性质可得EF是线段CP的垂直平分线，根据线段垂直平分线的性质可得PN=CN，所以∠CPN=∠PCN，即可得∠PCN=∠CPN=45°，根据三角形的内角和定理求得∠CNP=90°，又因∠CDP=90°，即可判定点C、D、P、N在以PC为直径的圆上，根据同弧所对的圆周角相等即可得∠NDC=∠NPC =45°．

（1）∵四边形ABCD是正方形，

∴BC=CD，∠BCD=∠CBG=∠D=90°，

∵BG=DP，

∴△BCG≌△DCP（SAS），

∴CP=CG，∠BCG=∠DCP，

∵∠PCG=45°，

∴∠BCG+∠DCP=45°，

∴∠DCP=∠BCG=22.5°，

∴∠PCF=∠PCG+∠BCG=67.5°，

在△PCG中，CP=CG，∠PCG=45°，

∴∠CPG=（180°﹣45°）÷2=67.5°

∴∠CPG =∠PCF，

∴PF=CF；

（2）如图，∵四边形ABCD是正方形，

∴∠CBG=∠BCD=90°，

过点C作CH⊥CG交AD的延长线于H，

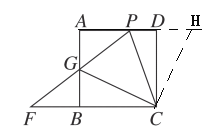
∴∠CDH=90°=∠HCG．

∴∠BCG=∠DCH，

∴△BCG≌△DCH（ASA），

∴CG=CH，

∵∠HCG=90°，∠PCG=45°，

∴∠PCH=45°=∠PCG，

∵CP=CP，

∴△PCH≌△PCG（SAS），

∴∠CPG=∠CPH，

∵∠CPD+∠DCP=90°，

∴∠CPF+∠DCP=90°，

∵∠PCF+∠DCP=90°，

∴∠CPF=∠PCF，

∴PF=CF；

（3）如图，连接PN，由（2）知，PF=CF，

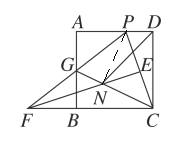
∵EF⊥CP，

∴PE=CE，

∴EF是线段CP的垂直平分线，

∴PN=CN，

∴∠CPN=∠PCN，

∵∠PCN=45°，

∴∠CPN=45°，

∴∠CNP=90°，

∵∠CDP=90°，

∴点C、D、P、N在以PC为直径的圆上，

∴∠NDC=∠NPC =45°．