题目内容
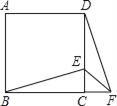
【题目】如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.
(1)△DCF可以看作是△BCE绕点C旋转某个角度得到的吗?
(2)若∠CEB=60°,求∠EFD的度数.
【答案】(1)△DCF可以看作是△BCE绕点C旋转90°而得到的图形;(2)∠EFD=15°.
【解析】试题分析:(1)可利用边角边证明△DCF≌△BCE,从而即可得;
(2)由(1)中的全等可得∠DFC=∠BEC=60°,易得∠CFE=45°,相减即可得到所求角的度数.
试题解析:(1)∵四边形ABCD是正方形,
∴DC=BC,∠DCB=∠FCE=90°,
在△DCF和△BCE中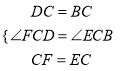 ,
,
∴△DCF≌△BCE(SAS),
∴△DCF可以看作是△BCE绕点C旋转90°而得到的图形;
(2)∵△BCE≌△DCF,
∴∠DFC=∠BEC=60°,
∵CE=CF,
∴∠CFE=45°,
∴∠EFD=15°.

练习册系列答案
相关题目
【题目】一病人发高烧进医院进行治疗,医生给他开了药并挂了水,同时护士每隔1小时对病人测体温,及时了解病人的好转情况,现护士对病人测体温的变化数据如下表:
时 间 | 7:00 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 |
体温 | 升0.2 | 降1.0 | 降0.8 | 降1.0 | 降0.6 | 升0.4 | 降0.2 | 降0.2 | 降0 |
注:病人早晨进院时医生测得病人体温是40.2℃。
问:(1)病人什么时候体温达到最高,最高体温是多少?
(2)病人中午12点时体温多高?
(3)病人几点后体温稳定正常?(正常体温是37℃)