ЬтФПФкШн
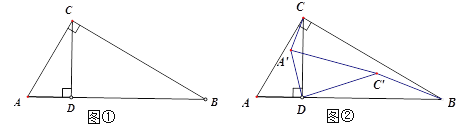
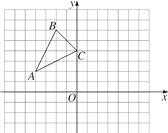
ЁОЬтФПЁПШчЭМ1ЃЌАбСНИіШЋЕШЕФШ§НЧАхABCЁЂEFGЕўЗХдквЛЦ№ЃЌЪЙШ§НЧАхEFGЕФжБНЧБпFGОЙ§Ш§НЧАхABCЕФжБНЧЖЅЕуCЃЌДЙжБABгкGЃЌЦфжаЁЯB=ЁЯF=30ЁуЃЌаББпABКЭEFОљЮЊ4ЃЎЯжНЋШ§НЧАхEFGгЩЭМ1ЫљЪОЕФЮЛжУШЦGЕубиФцЪБеыЗНЯђа§зЊ![]() ЃЈ0ЃМ
ЃЈ0ЃМ![]() ЃМ90ЁуЃЉЃЌШчЭМ2ЃЌEGНЛACгкЕуKЃЌGFНЛBCгкЕуHЃЎдка§зЊЙ§ГЬжаЃЌЧыФуНтОівдЯТЮЪЬтЃК
ЃМ90ЁуЃЉЃЌШчЭМ2ЃЌEGНЛACгкЕуKЃЌGFНЛBCгкЕуHЃЎдка§зЊЙ§ГЬжаЃЌЧыФуНтОівдЯТЮЪЬтЃК
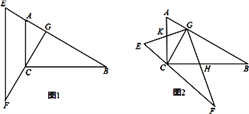
ЃЈ1ЃЉЧѓжЄЃКЁїCGHЁзЁїAGKЃЛ
ЃЈ2ЃЉСЌНгHKЃЌЧѓжЄЃКKHЁЮEFЃЛ
ЃЈ3ЃЉЩшAK=xЃЌЁїCKHЕФУцЛ§ЮЊyЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіyЕФзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮі;ЃЈ2ЃЉжЄУїМћНтЮі;ЃЈ3ЃЉy= ![]() , yзюДѓжЕЮЊ
, yзюДѓжЕЮЊ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉGHЃКGKЕФжЕУЛЗЂЩњБфЛЏЃЌИљОнвбжЊЬѕМўжЄУїЁїAGKЁзЁїCGHЃЌгЩЯрЫЦШ§НЧаЮЕФаджЪПЩЕУЃК ![]() =
=![]() ЃЌгжвђЮЊдкRtЁїACGжаЃЌtanЁЯA=
ЃЌгжвђЮЊдкRtЁїACGжаЃЌtanЁЯA=![]() =
=![]() ЃЌЫљвдGHЃКGKЕФБШжЕЪЧвЛИіЕФжЕ
ЃЌЫљвдGHЃКGKЕФБШжЕЪЧвЛИіЕФжЕ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСЌНгHKЃЌгЩЃЈ1ЃЉПЩжЊдкRtЁїKHGжаЃЌtanЁЯGKH=![]() =
=![]() ЃЌЫљвдЁЯGKH=60ЁуЃЌдйИљОнШ§НЧаЮЕФФкНЧКЭжЄУїЃЌЁЯE=ЁЯEGF-ЁЯF=90Ёу-30Ёу=60ЁуЃЌМДПЩжЄЕУЁЯGKH=ЁЯE=60ЁуЃЌРћгУЭЌЮЛНЧЯрЕШСНЯпЦНааМДПЩжЄУїKHЁЮEFЃЛ
ЃЌЫљвдЁЯGKH=60ЁуЃЌдйИљОнШ§НЧаЮЕФФкНЧКЭжЄУїЃЌЁЯE=ЁЯEGF-ЁЯF=90Ёу-30Ёу=60ЁуЃЌМДПЩжЄЕУЁЯGKH=ЁЯE=60ЁуЃЌРћгУЭЌЮЛНЧЯрЕШСНЯпЦНааМДПЩжЄУїKHЁЮEFЃЛ
ЃЈ3ЃЉЩшAK=xЃЌДцдкx=1ЃЌЪЙЁїCKHЕФУцЛ§зюДѓЃЌгЩЃЈ1ЃЉЕУЁїAGKЁзЁїCGHЃЌЫљвдCH=![]() AK=
AK=![]() xЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНБэЪОГіSЁїCHK=
xЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНБэЪОГіSЁїCHK=![]() CKCH=
CKCH=![]() ЃЈ2-xЃЉ
ЃЈ2-xЃЉ![]() xЃЌдйАбЖўДЮКЏЪ§ЕФНтЮіЪНЛЏЮЊЖЅЕуЪНМДПЩЧѓГіxЕФжЕЃЎ
xЃЌдйАбЖўДЮКЏЪ§ЕФНтЮіЪНЛЏЮЊЖЅЕуЪНМДПЩЧѓГіxЕФжЕЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉжЄУїЃКдкRtЁїABCжаЃЌCGЁЭABЃЌЁЯB=30ЁуЃЌ
ЁрЁЯGCH=ЁЯGAK=60Ёу.
гжЁЯCGH=ЁЯAGK= ![]() ЃЌ
ЃЌ
ЁрЁїCGHЁзЁїAGK.
ЃЈ2ЃЉжЄУїЃКСЌНгHKЃЌ

гЩЃЈ1ЃЉЕУЁїCGHЁзЁїAGKЃЌ
Ёр![]() .
.
дкRtЁїACGжаЃЌtanA=![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() .
.
дкRtЁїKHGжаЃЌtanЁЯGKH=![]() ЃЌ
ЃЌ
ЁрЁЯGKH=60Ёу.
ЁпRtЁїEFGжаЃЌЁЯF=30ЁуЃЌЁрЁЯE=60ЁуЃЌ
ЁрЁЯGKH=ЁЯEЃЌ
ЁрKHЁЮEF.
ЃЈ3ЃЉНтЃКгЩЃЈ1ЃЉЕУЁїCGHЁзЁїAGKЃЌ
Ёр![]()
гЩЃЈ2ЃЉжЊ![]() ЃЌЁр
ЃЌЁр![]() .
.
ЁрCH=![]() AK=
AK= ![]() .
.
дкRtЁїABCжаЃЌЁЯB=30ЁуЃЌ
ЁрAC=![]() AB=2ЃЌ
AB=2ЃЌ
ЁрCK=AC-AK=2-x.
Ёрy=![]() CKЁЄCH=
CKЁЄCH= ![]() =
= ![]() .
.
гжy=![]() .
.
ЁрЕБx=1ЪБЃЌyгазюДѓжЕЮЊ![]() .
.
ЕуОІ: БОЬтПМВщЕФЪЧЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪМАЭМаЮа§зЊЕФаджЪЁЂЦНааЯпЕФХаЖЈКЭаджЪЁЂШ§НЧаЮЕФУцЛ§ЙЋЪНЁЂЖўДЮКЏЪ§ЕФзюжЕЮЪЬтЃЌЬтФПЕФзлКЯадКмЧПЃЌФбЖШжаЕШЃЎ

 гРЧЌНЬг§КЎМйзївЕПьРжМйЦкбгБпШЫУёГіАцЩчЯЕСаД№АИ
гРЧЌНЬг§КЎМйзївЕПьРжМйЦкбгБпШЫУёГіАцЩчЯЕСаД№АИ