ΧβΡΩΡΎ»ί
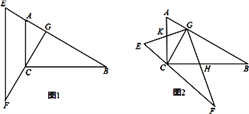
ΓΨΧβΡΩΓΩ»γΆΦΔΌΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90Γψ, ΓœB=30Γψ,AC=1,CDΓΆABΘ§¥ΙΉψΈΣDΘ§œ÷ΫΪΓςACD»ΤDΒψΥ≥ ±’κ–ΐΉΣ![]() ΒΟΒΫΓςAΓ°CΓ·D, –ΐΉΣ ±ΦδΈΣtΟκΘ§ΓςACD»ΤDΒψ–ΐΉΣΒΡΫ«ΥΌΕ»
ΒΟΒΫΓςAΓ°CΓ·D, –ΐΉΣ ±ΦδΈΣtΟκΘ§ΓςACD»ΤDΒψ–ΐΉΣΒΡΫ«ΥΌΕ»![]() /Οκ(ΟΩΟκΉΣ10Ε») Θ°
/Οκ(ΟΩΟκΉΣ10Ε») Θ°
Θ®1Θ©–ΐΉΣ ±Φδt= Οκ ±Θ§AΓ°CΓ·ΓΈAB;
Θ®2Θ©ΓςACD»ΤDΒψΥ≥ ±’κ–ΐΉΣ“Μ÷ήΘ®3600Θ©Θ§–±±ΏAC…®ΙΐΒΡΟφΜΐΈΣ ΘΜ
Θ®3Θ©»γΆΦΔΎΘ§Ν§Ϋ”AΓ·CΓΔ CΓ·BΘ°
ΔΌ»τ6ΘΦtΘΦ9Θ§«σ÷ΛΘΚ ![]() ΈΣΕ®÷ΒΘΜ
ΈΣΕ®÷ΒΘΜ
ΔΎΒ±tΘΨ9 ±Θ§…œ ωΫα¬έΜΙ≥…ΝΔ¬πΘΩ»γ≥…ΝΔ÷±Ϋ”–¥≥ω±»÷ΒΘ§≤Μ≥…ΝΔ«κΥΒΟςάμ”…Θ°
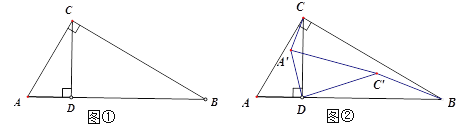
ΓΨ¥πΑΗΓΩΘ®1Θ©6Θ®2Θ©![]() Θ®3Θ©ΔΌ÷ΛΟςΦϊΫβΈωΘΜΔΎΫα¬έ≥…ΝΔΘ§±»÷Β»‘ΈΣ
Θ®3Θ©ΔΌ÷ΛΟςΦϊΫβΈωΘΜΔΎΫα¬έ≥…ΝΔΘ§±»÷Β»‘ΈΣ![]() .
.
ΓΨΫβΈωΓΩΖ÷ΈωΘΚΘ®1Θ©”…–ΐΉΣΒΡ–ΐΉΣΩ…ΒΟ»τ“Σ![]() ΓΈAB,Ω…
ΓΈAB,Ω…![]() ,Φ¥Ω…«σΫβΘΜΘ®2Θ©”…Χβ“βΩ…÷Σ–±±ΏAC…®ΙΐΒΡΟφΜΐΈΣ“‘ΒψDΈΣ‘≤–ΡCDΘ§AC±Ώ…œΒΡΗΏΈΣΑκΨΕΒΡΜΖ–ΈΘ§άϊ”Ο¥σ‘≤ΟφΜΐΦθ»Ξ–Γ‘≤ΟφΜΐΦ¥Ω…«σΫβΘΜΘ®3Θ©ΔΌΒ±6ΘΦtΘΦ9 ±Θ§÷Σ60ΓψΘΦΠΝΘΦ90ΓψΘ§”…Γς
,Φ¥Ω…«σΫβΘΜΘ®2Θ©”…Χβ“βΩ…÷Σ–±±ΏAC…®ΙΐΒΡΟφΜΐΈΣ“‘ΒψDΈΣ‘≤–ΡCDΘ§AC±Ώ…œΒΡΗΏΈΣΑκΨΕΒΡΜΖ–ΈΘ§άϊ”Ο¥σ‘≤ΟφΜΐΦθ»Ξ–Γ‘≤ΟφΜΐΦ¥Ω…«σΫβΘΜΘ®3Θ©ΔΌΒ±6ΘΦtΘΦ9 ±Θ§÷Σ60ΓψΘΦΠΝΘΦ90ΓψΘ§”…Γς![]() ΓΉΓς
ΓΉΓς![]() ΚΆΓς
ΚΆΓς![]() ΓΉΓς
ΓΉΓς![]() ΒΟΒΫ
ΒΟΒΫ![]() ΈΣΕ®÷Β
ΈΣΕ®÷Β![]() ΘΜΔΎ”Ο”κΔΌœύΆ§ΒΡΖΫΖ®Φ¥Ω…ΒΟ≥ωΫαΙϊ.
ΘΜΔΎ”Ο”κΔΌœύΆ§ΒΡΖΫΖ®Φ¥Ω…ΒΟ≥ωΫαΙϊ.
±ΨΧβΫβΈωΘΚ
Θ®1Θ©”…![]() ΓΈAB,ΒΟ
ΓΈAB,ΒΟ![]() Θ§Γύt=6.
Θ§Γύt=6.
Θ®2Θ©…ηAC±Ώ…œΒΡΗΏΈΣh,”…![]() .
.
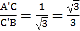
Θ®3Θ©ΔΌΒ±6ΘΦtΘΦ9 ±Θ§÷Σ600ΘΦ![]() ΘΦ900
ΘΦ900
»γΆΦΝ§Ϋ”AAΓ°ΓΔC CΓ·
”…–ΐΉΣΕ®“ε÷Σ
ΓœAD AΓ°=ΓœCD CΓ·=Γœ![]()
ΓΏAD=AΓ°DΓΔCD= CΓ°D
ΓύΓςADAΓ° ΓΉΓςC D CΓ°Θ°
ΓύΓœAΓ°A D =ΓœCΓ°CD ; ![]() ,
,
”÷ΓΏΓœCAD =ΓœBCD =60O
ΓύΓςACAΓ° ΓΉΓςC BCΓ·
Γύ![]() ΈΣΕ®÷Β.
ΈΣΕ®÷Β.
ΔΎΫα¬έ≥…ΝΔΘ§±»÷Β»‘ΈΣ![]() .
.
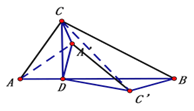

ΓΨΧβΡΩΓΩΈ¬÷ίΚΆΚΦ÷ίΡ≥≥ßΆ§ ±…ζ≤ζΡ≥÷÷–ΆΚ≈ΒΡΜζΤς»τΗ…Χ®Θ§Έ¬÷ί≥ßΩ…÷ß‘°ΆβΒΊ![]() Χ®Θ§ΚΦ÷ί≥ßΩ…÷ß‘°ΆβΒΊ
Χ®Θ§ΚΦ÷ί≥ßΩ…÷ß‘°ΆβΒΊ![]() Χ®Θ°œ÷‘ΎΨωΕ®ΗχΈδΚΚ
Χ®Θ°œ÷‘ΎΨωΕ®ΗχΈδΚΚ![]() Χ®Θ§Ρœ≤ΐ
Χ®Θ§Ρœ≤ΐ![]() Χ®Θ°ΟΩΧ®ΜζΤςΒΡ‘ΥΖ―Θ®ΒΞΈΜΘΚΑΌ‘ΣΘ©»γ±μΘ°…ηΚΦ÷ί‘ΥΆυΡœ≤ΐΒΡΜζΤςΈΣ
Χ®Θ°ΟΩΧ®ΜζΤςΒΡ‘ΥΖ―Θ®ΒΞΈΜΘΚΑΌ‘ΣΘ©»γ±μΘ°…ηΚΦ÷ί‘ΥΆυΡœ≤ΐΒΡΜζΤςΈΣ![]() Χ®Θ°
Χ®Θ°
Ρœ≤ΐ | ΈδΚΚ | |
Έ¬÷ί≥ß |
|
|
ΚΦ÷ί≥ß |
|
|
Θ®![]() Θ©”Ο
Θ©”Ο![]() ΒΡ¥ζ ΐ Ϋά¥±μ ΨΉή‘ΥΖ―Θ®ΒΞΈΜΘΚΑΌ‘ΣΘ©Θ°
ΒΡ¥ζ ΐ Ϋά¥±μ ΨΉή‘ΥΖ―Θ®ΒΞΈΜΘΚΑΌ‘ΣΘ©Θ°
Θ®![]() Θ©»τΉή‘ΥΖ―ΈΣ
Θ©»τΉή‘ΥΖ―ΈΣ![]() ‘ΣΘ§‘ρΚΦ÷ί‘ΥΆυΡœ≤ΐΒΡΜζΤς”ΠΈΣΕύ…ΌΧ®?
‘ΣΘ§‘ρΚΦ÷ί‘ΥΆυΡœ≤ΐΒΡΜζΤς”ΠΈΣΕύ…ΌΧ®?
Θ®![]() Θ© ‘Έ ”–ΈόΩ…Ρή ΙΉή‘ΥΖ― «
Θ© ‘Έ ”–ΈόΩ…Ρή ΙΉή‘ΥΖ― «![]() ‘Σ?»τ”–Ω…ΡήΘ§«κ–¥≥ωœύ”ΠΒΡΒς‘ΥΖΫΑΗΘΜ»τΈόΩ…ΡήΘ§«κΥΒΟςάμ”…Θ°
‘Σ?»τ”–Ω…ΡήΘ§«κ–¥≥ωœύ”ΠΒΡΒς‘ΥΖΫΑΗΘΜ»τΈόΩ…ΡήΘ§«κΥΒΟςάμ”…Θ°