题目内容
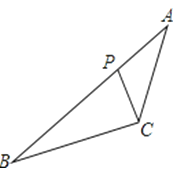
【题目】如图,△ABC中,如果AB=30cm,BC=24cm,AC=27cm,AE=EF=FB,EG∥DF∥BC,FM∥EN∥AC,则图中阴影部分的三个三角形周长之和为( )
A.70
B.75
C.81
D.80
【答案】C
【解析】根据已知可求得△ABC的周长,由题意得,△DNC与△ABC相似,且相似比是1:3,从而可得到阴影部分的周长和等于△ABC的周长,即得到了答案.
∵AB=30cm,BC=24cm,AC=27cm
∴△ABC的周长是81cm
∵AE=EF=FB,EG∥DF∥BC,FM∥EN∥AC,
∴AG=DG=DC,CN=NM=MB,
即![]() =
=![]() ,
,
又∵∠A=∠A.
∴△DNC∽△ABC,且相似比是1:3
∴周长的比是1:3
∴三个三角形的周长的和等于△ABC的周长
∴阴影部分的三个三角形的周长的和是81cm.
故选C.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目