题目内容
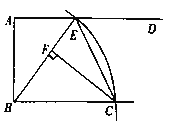
【题目】如图,长方形纸片ABCD(AD>AB),点O位于边BC上,点E位于边AB上,点F位于边AD上,将纸片沿OE、OF折叠,点B、C、D的对应点分别为B′、C′、D′.
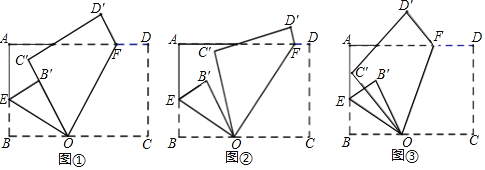
(1)将长方形纸片ABCD按图①所示的方式折叠,若点B′在OC′上,则∠EOF的度数为 ;(直接填写答案)
(2)将长方形纸片ABCD按图②所示的方式折叠,若∠B′OC′=20°,求∠EOF的度数;(写出必要解题步骤)
(3)将长方形纸片ABCD按图③所示的方式折叠,若∠EOF=x°,则∠B′OC′的度数为 .(直接填写答案,答案用含x的代数式表示.
【答案】(1)100°;(2)100°;(3)180°﹣2x°
【解析】
(1)依据折叠的性质,即可得到∠BOE=∠B'OE,∠COF=∠C'OF,进而得出∠EOF=90°;
(2)设∠BOE=∠B'OE=x,∠C'OF=∠COF=y,得出x+y=80°,进而得出答案;
(3)设∠BOE=∠B'OE=α,∠C'OF=∠COF=β,得出α+β=180°﹣x°,由∠EOF=∠EOB'﹣∠B'OC'+∠C'OF=α﹣∠B'OC'+β,进而得出答案.
(1)由折叠的性质得:∠BOE=∠B'OE,∠COF=∠C'OF,
∵点B′在OC′上,
∴∠EOF=![]() (∠BOC'+∠COC')=
(∠BOC'+∠COC')=![]() ×180°=90°,
×180°=90°,
故答案为:90°;
(2)∵沿OE、OF折叠,
∴设∠BOE=∠B'OE=x,∠C'OF=∠COF=y,
∵2x+20°+2y=180°,
∴x+y=80°,
∴∠EOF=x+20°+y=20°+80°=100°;
(3)∵沿OE、OF折叠,
∴设∠BOE=∠B'OE=α,∠C'OF=∠COF=β,
∴∠EOF=180°﹣∠BOE﹣∠COF=180°﹣(α+β),
即α+β=180°﹣x°,
又∵∠EOF=∠EOB'﹣∠B'OC'+∠C'OF=α﹣∠B'OC'+β,
∴∠B'OC'=(α+β)﹣∠EOF=180°﹣x°﹣x°=180°﹣2x°,
故答案为:180°﹣2x°.

 高效智能课时作业系列答案
高效智能课时作业系列答案