题目内容
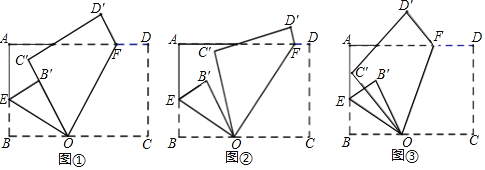
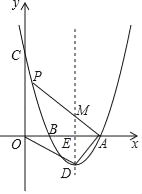
【题目】如图,抛物线y=mx2﹣8mx+12m(m>0)与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C,顶点为D,其对称轴与x轴交于点E,联接AD,OD.
(1)求顶点D的坐标(用含m的式子表示);
(2)若OD⊥AD,求该抛物线的函数表达式;
(3)在(2)的条件下,设动点P在对称轴左侧该抛物线上,PA与对称轴交于点M,若△AME与△OAD相似,求点P的坐标.
【答案】(1)顶点D的坐标为(4,﹣4m);(2)y=![]() x2﹣4
x2﹣4![]() x+6
x+6![]() ;(3)点P的坐标(0,6
;(3)点P的坐标(0,6![]() )或(1,
)或(1,![]() ).
).
【解析】分析:(1)把抛物线解析式配成顶点式得到D点坐标;
(2)先解方程mx2-8mx+12m=0得到A(6,0),B(2,0),再证明△DEO∽△AED,利用相似比得到4m:2=4:4m,然后求出m即可得到抛物线解析式;
(3)由(2)得D(4,-2![]() ),利用相似的传递性得到△AME与△EAD相似,由于∠ADO=∠AEM=90°,根据相似三角形的判定,当
),利用相似的传递性得到△AME与△EAD相似,由于∠ADO=∠AEM=90°,根据相似三角形的判定,当![]() 时,△AEM∽△DEA,即
时,△AEM∽△DEA,即![]() ,解得EM=
,解得EM=![]() ,当
,当![]() ,则EM=DE=2
,则EM=DE=2![]() ,则EM=DE=2
,则EM=DE=2![]() ,分别确定对应M点的坐标,求出相应直线AM的解析式,然后把直线AM的解析式与抛物线解析式组成方程组,再解方程组可得到对应P点坐标.
,分别确定对应M点的坐标,求出相应直线AM的解析式,然后把直线AM的解析式与抛物线解析式组成方程组,再解方程组可得到对应P点坐标.
详解:(1)∵y=m(x﹣4)2﹣4m,
∴顶点D的坐标为(4,﹣4m);
(2)当y=0时,mx2﹣8mx+12m=0,解得x1=2,x2=6,
∴A(6,0),B(2,0),
∴OA=6,
∵抛物线的对称轴为x=4,
∴点E(4,0),
则OE=4,AE=2,DE=4m,
∵OD⊥AD,
∴∠ADO=90°,即∠ODE+∠ADE=90°,
而∠ODE+∠DOE=90°,
∴∠DOE=∠ADE,
∴△DEO∽△AED,
∴DE:AE=OE:DE,即4m:2=4:4m,解得m1=![]() ,m2=﹣
,m2=﹣![]() (舍去),
(舍去),
∴抛物线解析式为y=![]() x2﹣4
x2﹣4![]() x+6
x+6![]() ;
;
(3)由(2)得D(4,﹣2![]() ),
),
∵△ADO与△AED相似,△AME与△OAD相似
∴△AME与△EAD相似,
∵∠ADO=∠AEM=90°,
∴当![]() 时,△AEM∽△DEA,即
时,△AEM∽△DEA,即![]() ,解得EM=
,解得EM=![]() ,
,
∴M(4,![]() )
)
易得直线AM的解析式为y=﹣![]() x+3
x+3![]() ,
,
解方程组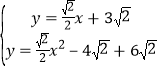 得
得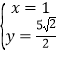 或
或![]() ,
,
∴此时P点坐标为(1,![]() ),
),
当![]() ,则EM=DE=2
,则EM=DE=2![]() ,
,
∴M(4,2![]() ),
),
易得直线AM的解析式为y=﹣![]() x+6
x+6![]() ,
,
解方程组 得
得![]() 或
或![]() ,
,
∴此时P点坐标为(0,6![]() ),
),
综上所述,点P的坐标(0,6![]() )或(1,
)或(1,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案