Question

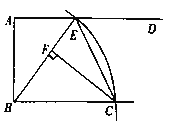
【题目】如图所示,AD∥BC,∠BAD=90°,以B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过C作CF⊥BE于点F.

(1)线段BF与图中哪条线段相等?写出来并加以证明;

（2）若AB=12,BC=13,P从E沿ED方向运动,Q从C出发向B运动,两点同时出发且速度均为每秒1个单位

①当 秒时,四边形EPCQ是矩形

②当 秒时,四边形EPCQ是菱形

Answer 1

【答案】BF=AE，证明见解析；(2)①8②13

【解析】试题分析：

（1）由已知条件易得BE=BC，∠A=∠BFC=90°，再证∠ABE=∠FCB，即可得到△ABE≌△FCB，从而可得BF=AE；

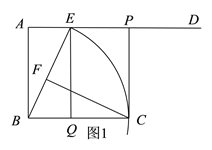
（2）①如图1，由已知易得四边形EPCQ是平行四边形，故当EQ⊥BC时，四边形EPCQ是矩形，在Rt△AEQ中由勾股定理易得BQ=5，从而可得CQ=8，由此即可得到点Q的运动时间了；

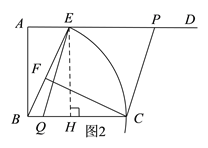
②同①可知，四边形EPCQ是平行四边形，由此可知当QE=PE时，四边形EPCQ是菱形，过点E作EH⊥BC于点H，在Rt△EQH中由勾股定理结合已知条件即可求出运动时间x.

试题解析：

(1)BF=AE.理由如下:

由题可知∠A=∠BFC=90°,BC=BE

∵AD∥BC,∴∠AEB=∠FBC.

∴△ABE≌△FCB.

∴AE=BF

(2)①如图1，当EQ⊥BC时，四边形EPCQ是矩形，

此时在Rt△AEQ中，∵∠BQE=90°，BE=BC=13，QE=AB=12，

∴由勾股定理可得：BQ=5，

∴CQ=BC-BQ=13-5=8，

∴当第8秒时，四边形EPCQ是矩形；

②如图2，设运动时间为x秒，由题意可得四边形EPCQ是平行四边形，故当QE=PE=x时，四边形EPCQ是菱形，过点E作EH⊥BC于点H，由①可知，BH=AE=5，EH=AB=12，

∴CH=BC-BH=13-5=8，则QH=CQ-CH=x-8，

∴在Rt△EQH中由勾股定理可得： ，解得： ，

即当运动13秒时，四边形EPCQ是菱形.