题目内容
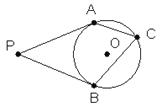
【题目】如图, PA、PB是⊙O的切线,切点为A、B,C是⊙O上一点(P与A、B不重合),若∠P=52°,则∠ACB=______________度.
【答案】64或116
【解析】
连接OA、OB.根据切线的性质,得到∠OAP=∠OBP=90°,根据四边形的内角和定理即可求得∠AOB,再进一步根据圆周角定理求解即可,同列得出C点在劣弧AB上时,求出∠ACB的度数即可.
连接OA、OB,
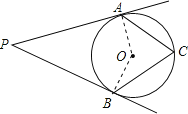
∵PA、PB是⊙O的切线,切点分别为A、B,
∴∠OAP=∠OBP=90°(切线的性质).
∵∠P=52°(已知),
∴∠AOB=180°-∠P=128°(四边形的内角和定理),
∴∠ACB=![]() ∠AOB=64°(同弧所对的圆周角是所对的圆心角的一半).
∠AOB=64°(同弧所对的圆周角是所对的圆心角的一半).
同理可得出:当C点在劣弧AB上时,∠ACB的度数为:180°-64°=116°.
故答案为:64或116.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目