题目内容
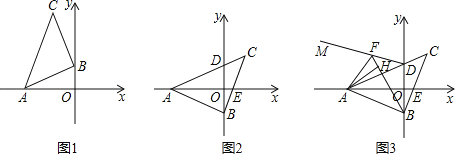
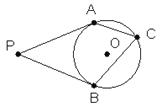
【题目】如图,锐角![]() 的两条高
的两条高![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() .
.
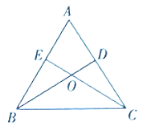
(1)证明:![]() .
.
(2)判断点![]() 是否在
是否在![]() 的角平分线上,并说明理由.
的角平分线上,并说明理由.
(3)连接![]() ,
,![]() 与
与![]() 是否平行?为什么?
是否平行?为什么?
【答案】(1)见解析(2)点O在∠BAC的角平分线上,理由见解析(3)平行,理由见解析
【解析】
(1)根据题意证明△BCE≌△CBD即可求解;
(2)由(1)得到△ABC为等腰三角形,连接AO并延长交BC于F,通过证△AOE≌△AOD,得到∠BAF=∠CAF,即点O在∠BAC的角平分线上.
(3)连接![]() ,根据等腰三角形三线合一即可求解.
,根据等腰三角形三线合一即可求解.
(1)∵锐角![]() 的两条高
的两条高![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]()
BC=CB,
∴△BCE≌△CBD(HL)
∴![]()
(2)解:点O在∠BAC的角平分线上.
理由:∵△BCE≌△CBD
∴∠EBC=∠DCB,BE=CD
∴△ABC为等腰三角形,
∴AB=AC,
则AB-BE=AC-CD
∴AE=AD
连接AO并延长交BC于F,
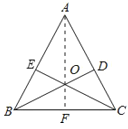
在Rt△AOE和Rt△AOD中,
![]()
∴Rt△AOE≌Rt△AOD.
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上.
(3)平行,理由如下:
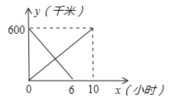
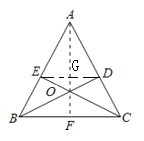
如图,连接![]() ,交AF于G点,
,交AF于G点,
∵AE=AD
∴△ADE为等腰三角形,
由(2)得到AF为∠BAC的角平分线
∴AG⊥DE,
又AF⊥BC,
∴DE∥BC.

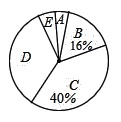
【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组 | 视力 | 人数 |
A | 3.95≤x≤4.25 | 2 |
B | 4.25<x≤4.55 | |
C | 4.55<x≤4.85 | 20 |
D | 4.85<x≤5.15 | |
E | 5.15<x≤5.45 | 3 |
根据以上信息,解答下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人,在4.25<x≤4.55范围内的学生数占被调查的学生数的百分比为 %.
(2)本次调查的样本容量是 ,视力在4.85<x≤5.15范围内的学生数占被调查学生数的百分比是 %.
(3)本次调查中,视力的中位数落在 组.
(4)若该校九年级有350名学生,估计视力超过4.85的学生数.