Question

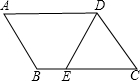
如图，在?ABCD中，点F是边BC的中点，连接AF并延长交DC的延长线于点E，连接AC、BE．
（1）求证：CE=CD；
（2）若∠AFC=2∠D，则四边形ABEC是怎样的特殊四边形？请证明你的结论．

Answer 1

（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∴∠ABF=∠ECF，
∵点F是边BC的中点，
∴BF=CF，
在△ABF和△CEF中，

∠ABF=∠ECF BF=CF ∠AFB=∠EFC

，
∴△ABF≌△ECF（ASA），
∴CE=AB，
∴CE=CD；

（2）四边形ABEC是矩形．
理由：∵AB∥CD，AB=CE，
∴四边形ABEC是平行四边形，
∴AE=2AF，BC=2BF，
∵四边形ABCD是平行四边形，
∴∠ABF=∠D，
∵∠AFC=2∠D，∠AFC=∠ABF+∠BAF，
∴∠ABF=∠BAF，
∴AF=BF，
∴AE=BC，
∴四边形ABEC是矩形．