题目内容
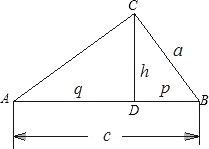已知：如图，CD是Rt△ABC的斜边AB上的高，且BC=a，AB=c，CD=h，AD=q，DB=p．求证：h2=p•q，a2=p•c．
分析：欲证：h2=p•q，可以证明Rt△ADC∽Rt△CDB得出，欲证a2=p•c，可以证明Rt△CDB∽Rt△ACB得出．
解答：证明：Rt△ABC，CD⊥AB，
∴∠ADC=∠CDB=90°，∠ACD=90°，
∴∠ACD+∠BCD=90°，∠ACD+∠A=90°，
∴∠BCD=∠A，
∴Rt△ADC∽Rt△CDB，
∴
=
?
=
，
∴h2=p•q；
同理可证Rt△CDB∽Rt△ACB，
得：a2=p•c．
∴∠ADC=∠CDB=90°，∠ACD=90°，
∴∠ACD+∠BCD=90°，∠ACD+∠A=90°，
∴∠BCD=∠A，
∴Rt△ADC∽Rt△CDB，
∴
| AD |
| CD |
| CD |
| BD |
| q |
| h |
| h |
| p |
∴h2=p•q；
同理可证Rt△CDB∽Rt△ACB，
得：a2=p•c．
点评：乘积的形式通常可以转化成比例的形式，通过相似三角形的性质得出．
练习册系列答案
相关题目
已知：如图，CD是⊙O的直径，点A在CD的延长线上，AB切⊙O于点B，若∠A=30°，OA=10，则AB=
1、已知：如图，CD是⊙O的直径，AE切⊙O于点B，DC的延长线交AB于点A，∠A=20°，则∠DBE=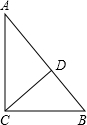
已知：如图，CD是△ABC的高，AC=4，BC=3，DB=
（2006•河北区一模）已知，如图，CD是⊙O的直径，BC是⊙O的切线，切点为C，BC=
已知，如图，CD是Rt△FBE的中位线，A是EB延长线上一点，AD∥BC．