题目内容
如图,已知点E、F是平行四边形ABCD对角线上的两点,请添加一个条件 使△ABE≌△CDF(只填一个即可).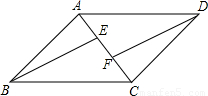
【答案】分析:根据平行四边形性质推出AB=CD,AB∥CD,得出∠BAE=∠DCF,根据SAS证两三角形全等即可.
解答:解:添加的条件是AE=CF,
理由是:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵在△ABE和△CDF中
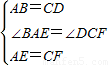 ,
,
∴△ABE≌△CDF,
故答案为:AE=CF.
点评:本题考查了平行四边形的性质和全等三角形的判定的应用,通过做此题培养了学生的分析问题和解决问题的能力,也培养了学生的发散思维能力,题目比较好,是一道开放性的题目,答案不唯一.
解答:解:添加的条件是AE=CF,
理由是:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵在△ABE和△CDF中
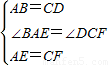 ,
,∴△ABE≌△CDF,
故答案为:AE=CF.
点评:本题考查了平行四边形的性质和全等三角形的判定的应用,通过做此题培养了学生的分析问题和解决问题的能力,也培养了学生的发散思维能力,题目比较好,是一道开放性的题目,答案不唯一.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 如图,已知点P、C是函数y=
如图,已知点P、C是函数y=| 1 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、S1与S2的大小不能确定 |
 什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
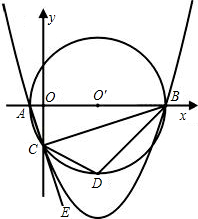
什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标. 如图,已知点A的坐标是(-1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
如图,已知点A的坐标是(-1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线. (2012•黑龙江)如图,已知点E、F是平行四边形ABCD对角线上的两点,请添加一个条件
(2012•黑龙江)如图,已知点E、F是平行四边形ABCD对角线上的两点,请添加一个条件 如图,已知点C、D是线段AB上两点,D是AC的中点,若CB=4cm,DB=7cm,求线段AB的长.
如图,已知点C、D是线段AB上两点,D是AC的中点,若CB=4cm,DB=7cm,求线段AB的长.